历史笔记迁移系列
Word转markdown真的好累
第一集:优化算法の笔记(上)- First Order Methods
第二集:优化算法の笔记(中) - Duality Method & Seconds Order Methods
第三集:优化算法の笔记(下) - ADMM & Coordinate Descent
0x04 Dual Methods and Application
我们回忆一下,给定一个函数$f$,他的共轭函数定义为:
\[f^*(y) = \max_{x} y^Tx - f(x)\]共轭函数是关于$y$的一些凸函数的逐点上确界,下面是他的一些性质:
- 对于任意的$x,y$,满足$f(x) + f^{*}(y) \le x^{T}y$
- 对于任意函数$f$,他的共轭函数的共轭函数,值不大于原函数:$f^{**}(x) \le f(x)$
- 如果函数$f$是凸的或者凹的,那上面两个性质都可以取等号,并且,满足$x \in \partial f*(y) \leftrightarrow x \in \arg\min _{z} f(z) - y^{T}z$。
共轭函数常常用于推导问题的对偶形式,但是实际上,当我们很想用对偶来求解问题的时候,这个共轭函数却不给力了,表现为很难给出一个闭式解来推得对偶形式,这时候就是dual-based subgradient or gradient methods起作用的时候了。考虑下面的优化目标,其中,$f$是closed的凸函数
\[\min_x f(x) \\ s.t. Ax=b\]构造Lagrangian multiplier,可以求出其对偶形式为下式,其中$f^*$是共轭函数,记$f* (-A^{T} u)=g(u), ∂g(u)=-A∂f* (-A^{T} u)$。
\[\max_u -f^*(-A^Tu) - b^Tu = -g(u) - b^Tu\]Dual subgradient算法就在于处理,我们无法直接求出对偶形式的最大值的时候,我们通过subgradient的方式进行求解,此时对偶问题的subgradient为$∂g(u)-b$。那么接下来顺着subgradient的迭代,我们就可以得到对偶问题的最优值。为了进行下一步的求解,这里是用到了共轭函数具有以下的性质,即
\[x \in \partial f^*(y) \leftrightarrow x \in arg\min_z f(z) - y^Tz\\ x \in \partial f^*(-A^Tu) \leftrightarrow x \in arg\min_z f(z) + u^TAz\]所以,dual subgradient的算法步骤为
- 首先确定一个初始的$u_{0}$
- 反复迭代直到满足停止准则
其中,第一个式子在于找出一个满足subgradient的点,第二步进行迭代更新,$t_{k}$是步长,当$f$函数是严格凸函数的时候,他的共轭函数是可微的,那么次梯度就等于梯度值。当然迭代更新的时候也可以使用proximal subgradient的加速方法。另一方面,dual subgradient的收敛性和primal gradient在本质上是相等的。 注意,在第一个式子中,我们需要求式子的最小值,这取决于$f$函数的形式是否简单。如果$f$函数是很多个函数的和呢? 即$f(x)=\sum f_{i}(x)$,此时我们可以考虑小批量的梯度下降,但是,如果$f$函数变成下面这个形式,每个子函数与特定的某部分的x有关。
\[f(x) = \sum^B_{i=1} f_i(x_i)\] 如果没有等式约束$Ax=b$,那么就可以并行的分块求解,在有约束的情况下,现在我们的优化问题变成下式,即已知变量$x=(x_{1},…,x_{B}) \in R^{n}$,$x_{i} \in R^{n_{i}}$, $\sum_{i=1}^{B} n_{i} =n$,被分割成$B$块,$A=[A_{1}, …, A_{B}]$,$A_{i} \in R^{m* n_{i}}$。
\[\min_x \sum_{i=1}^B f_i(x_i) \\ s.t. Ax=\sum_{i=1}^{B} A_ix_i = b\]带入到之前的dual subgradient式子中
\[x \in \partial f^*(-A^Tu) \leftrightarrow x \in \arg\min_z \sum_{i=1}^B f_i(z_i) + u^TAz \leftrightarrow x_i \in \arg\min_z \sum_{i=1}^B f_i(z_i) + u^TA_iz_i\]可以看到最后的形式,相当于是解B个子问题,这就是dual decomposition algorithm,其步骤为
\[x^k_i \in arg\min_{x_i} f_i(x_i) + (u^{k-1})^TA_ix_i\\ u^k = u^{k-1} + t_k (\sum_{i=1}^B A_ix_i^k - b)\]这个过程很像概率图模型中的belief propagation的思想: (Broadcast step)首先把第$k-1$次的$u$值同时赋值给$B$个子问题或叫sub-processor,之后每个sub-processor分别并行的更新$x_{i}$ (Gather step)最后各个部分的$x_{i}$集合起来再次更新$u^{k}$
另外,对于不等式约束也同样适用,此时问题变成下式。为了对他进行求解,不能再使用subgradient method,因为此时对偶变量$u$有了大于零的限制,所以可以采用projected subgradient method(也就是当$h(x)$是指示函数时候的proximal subgradient method)
\[\min_x \sum_{i=1}^B f_i(x_i) \\ s.t. \sum_{i=1}^{B} A_ix_i \le b\]projected subgradient method相当于是在凸集上的投影,所以更新方式是

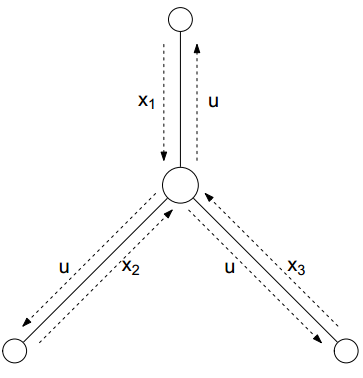
这个问题以系统资源占用为例,系统中有$B$个进程,每个进程有自己的决策变量$x_{i}$来决定需要哪些资源,需要多少资源,系统资源的多少限制记为$A$,资源$j$的价格记为$u_{j}$,此时更新过程为下式。如果资源$j$被过度使用,$s_{j}<0$,则提高价格$u_{j}$,反之若资源$j$没咋被使用,就降低$u_{j}$,过程中一直保证资源$j$是非负的。
\[u_j^+ = (u_j -ts_j)_+\\ s= b-\sum_{i=1}^B A_ix_i \\ where \quad (a)_+ = max(0,a)\]但是dual methods是通过对对偶问题进行求解,以收敛到原问题的解,但是传说这个需要很强的假设才行,而且即使在一定条件下对偶变量收敛了,原问题的迭代可能还是会不收敛,或者收敛点不符合约束条件,这时候就是Augmented Lagrangian method上场了,该算法首先把原问题转化为下式
\[\min_x f(x) + \frac{\rho}{2} \|Ax-b\|^2_2\\ s.t. Ax=b\]这附加项并不会改变问题的解,因为在任意可行解的情况下,他是等于0的。之后的步骤就是和dual subgradient方法差不多了:
\[x^k \in \arg\min_x f(x) + (u^{k-1})^T Ax + \frac{\rho}{2} \|Ax -b \| ^2_2\\ u^k = u^{k-1} + \rho (Ax^{k-1} - b)\]这里需要注意的是,在第二项中的迭代步长是恒为$ρ$,因为对于第一项的最小化有
\[0 \in \partial f(x^k) + A^T \left( u^{k-1} + \rho (Ax^k -b) \right) = \partial f(x^k) + A^Tu^k\] 这个式子,正好是原问题KKT条件中的stationary condition,这使得在$u^{k}$的迭代中,$x^{k}$也同时慢慢的达到最优,所以较一般的dual subgradient方法来说,具有更好的收敛性,但是由于附加项$\frac{ρ}{2} |Ax-b|_{2}^{2}$,并不具有可分性,所以这个方法不具有dual decomposition。 有没有同时保证收敛和对偶分解的算法呢?答案就是ADMM(Alternating Direction Method of Multipliers)。
0x04_1 ADMM
首先来看看下面这个问题
\[\min_x f_1(x_1) + f_2(x_2)\\ s.t. A_1x_1+A_2x_2=b\]接下来转换为Augmented form
\[\min_xf_1 (x_1 )+f_2 (x_2 )+\frac{ρ}{2} \|A_1 x_1+A_2 x_2-b\|_2^2\\ s.t. A_1 x_1+A_2 x_2=b\]他的Lagrangian为
\[L(x_1,x_2,u)=\min_x f_1 (x_i )+f_2 (x_2 )+\frac{ρ}{2} \|A_1 x_1+A_2 x_2-b\|_2^2+u^T (A_1 x_1+A_2 x_2-b)\]ADMM的更新方法为:
\[x_1^{k}=\arg\min_{x_1} L(x_1,x_2^{k-1},u^{k-1} )\\ x_2^{k}=\arg\min_{x_2} L(x_1^k,x_2,u^{k-1} )\\ u^k=u^{k-1}+ρ(A_1 x_1^k+A_2 x_2^k-b)\]一般来说,还可以令$w=\frac{u}{ρ}$,此时有
\[x_1^k=\arg\min_{x_1} f_1 (x_1 )+\frac{ρ}{2} \|A_1 x_1+A_2 x_2^{k-1}-b+w^{k-1} \|_2^2\\ x_2^k=\arg\min_{x_2} f_2 (x_2 )+\frac{ρ}{2} \|A_1 x_1^k+A_2 x_2-b+w^{k-1} \|_2^2\\ w^{k}=w^{k-1}+A_1 x_1^k+A_2 x_2^k-b=w^0+∑_{i=1}^k \left(A_1 x_1^i+A_2 x_2^i-b \right)\]由于附加项$\frac{ρ}{2} |A_1 x_1+A_2 x_2-b|_2^2$的存在,ADMM确实不能完全做decomposition,但是他可以近似的分解,也算是一种折中。并且参数$ρ$的选择也很重要,如果$ρ$太小,可能会得不到可行解,如果$ρ$太大,算法将忽略原始问题最小化$f(x)$。一般的办法就是多试试(祝你好运)
我们以Generalized lasso regression为例,看看ADMM是怎么做的。给定下面的优化问题:
\[\min_{\beta} f(\beta) + \lambda \|D\beta\|_1 \rightarrow \min_{\beta} f(\beta) + \lambda \|\alpha\|_1 \quad s.t. D\beta = \alpha\]他对应的ADMM算法更新式子为:
\[β^k=(X^T X+ρD^T D)^+ (X^T y+ρD^T (a^{k-1}-w^{k-1} ))\\ a^k=S_{λ/ρ} (Dβ^k+w^{k-1} )\\ w^k=w^{k-1}+Dβ^k-a^k\]另外,基于分布式环境下的ADMM算法也是业界常用的算法,算法的更多介绍可以访问
0x04_2 Coordinate Descent
我们再来讲讲另外一个更常用的算法:Coordinate Descent,又叫做Coordinatewise Minimization,是一种简单,高效并且很常用的优化方法。用来处理直接求解很复杂,但是如果只限制在一个维度的情况下则变得很简单甚至可以直接求极值的情况。
给定下面的优化问题:给定函数$g$是可微的凸函数,$h$是凸函数
\[\min f(x) = g(x) + \sum_{i=1}^n h_i(x_i)\]Coordinate Descent运行我们沿着坐标轴一维一维的优化。首先初始化$x^0$,在第k次迭代中执行每个维度的更新
\[x_1^k \in \arg\min_{x_1} f(x_1, x_2^{k-1}, ..., x_n^{k-1})\\ x_2^k \in \arg\min_{x_1} f(x_1^k, x_2, ..., x_n^{k-1})\\ x_n^k \in \arg\min_{x_1} f(x_1^k, x_2^k, ..., x_n)\]这种更新策略已经在ADMM算法中用到,但是coordinate descent不一定能达到最优解。
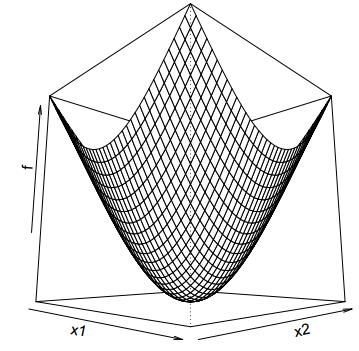
现在先考虑$f(x)$是可微的凸函数。假设最小值在$x^*$处取得,即$f(x^* )=\min_{z} f(z)$,令$e_{i}=(0,0,…,1,…,0) \in R^{n}$,表示第$i$个坐标轴方向,那么对于任意$i,δ$有(凸函数的一阶充要条件):
 |
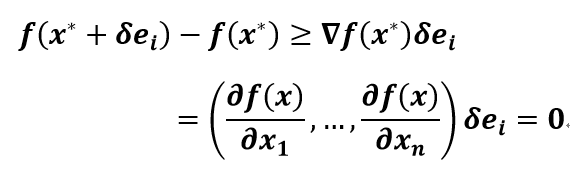 |
|---|---|
对于一般的不可微的凸函数来说,却不一定能收敛到最优解
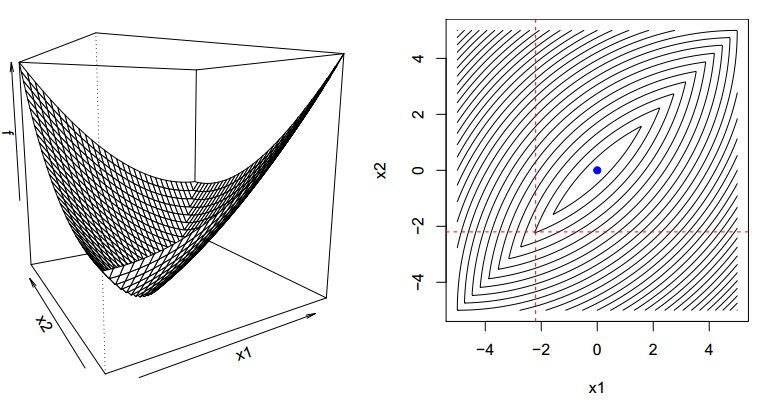
如上图在两条虚线相交的点处,每次再按照坐标方向寻最优已经收敛不到蓝色点的最小值处。然而对于,一开始目标形式的凸函数$\min f(x)=g(x)+∑{i=1}^{n} h{i} (x_{i}$来说是可以收敛到最优的,此时$h$函数那部分被称为separable。
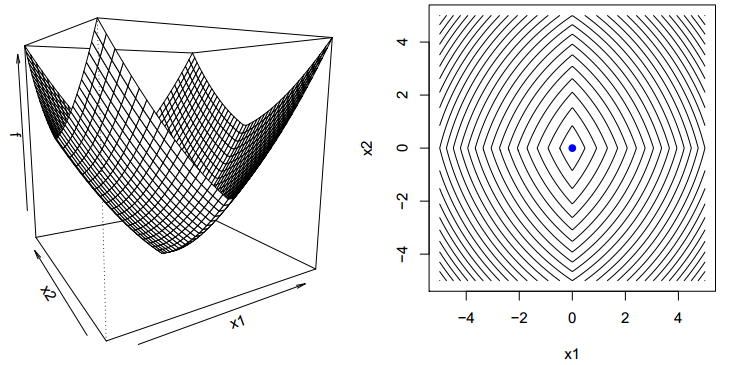
此时对于任意的$y=x^{*}+δe_{i}$有下式成立
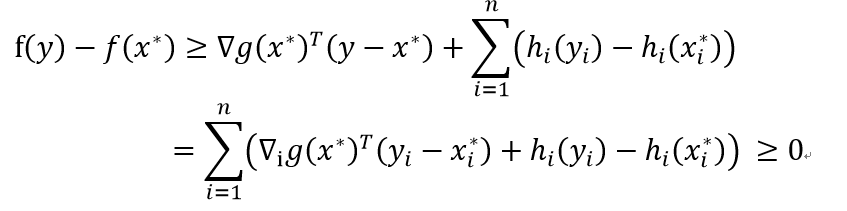
下面有一些例子,可以帮助大家更好的理解。
Linear Regression
给定下面的优化问题,其中$y\in R^{n},X=[X_{1},X_{2},..,X_{p}] \in R^{n,p}$
\[\min_{\beta} \frac{1}{2} \| y-X\beta\|_2^2\]由于目标问题可微,直接对$β_{i}$求导得
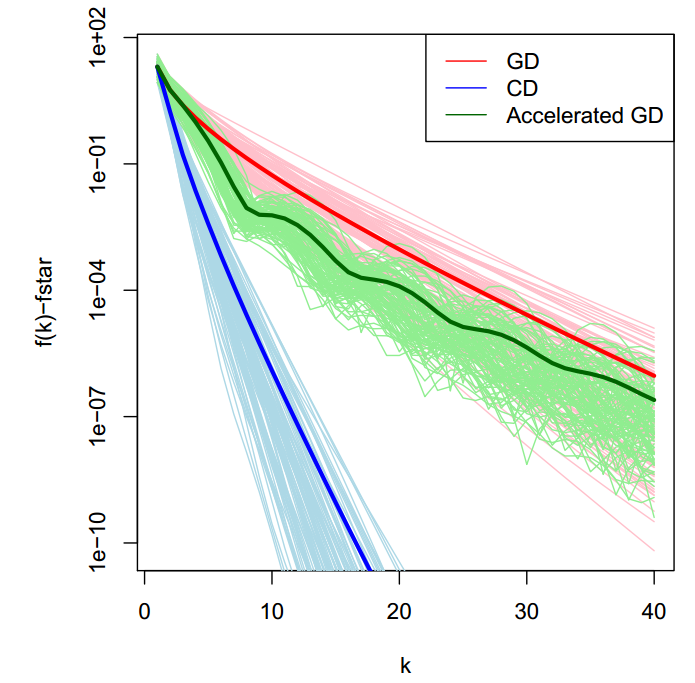
\[0=∇_i f(β)=X_i^T (Xβ-y)=X_i^T (X_i β_i+X_{-i} β_{-i}-y) → β_i=\frac{X_i^T (y -X_{-i} β_{-i} )}{X_i^T X_i}\]下图是蓝色是coordinate descent与gradient descent,Accelerated gradient descent的比较,明显它很快,但是coordinate descent并不是一阶的算法
SVM (SMO算法)
给定经典的SVM算法
\[\min_{\beta,\beta_0,\delta} \frac{1}{2} \|\beta\|_2^2 + C \sum_{i=1}^n \delta_{i} \\ s.t. \quad -\delta_i \le 0,i=1,2,...,n\\ \quad 1-\delta_i-y_i(x_i^T\beta + \beta_0) \le 0, i=1,2,...,n\]和它的对偶形式
\[\max_{w} -\frac{1}{2}W^T\hat{X}\hat{X}^TW + W^T1 \\ s.t. \quad 0\le w_i \le C, i=1,2,...,n\\ \quad W^Ty=0\]著名的SMO算法是典型的blockwise coordinate descent,具体来说是two blocks,并且贪心的选择不满足KKT条件的block进行更新而不是简单的坐标循环更新。对于SVM问题的KKT条件为
Stationary:$\sum_{i=1}^{n}w_{i}y_{i}=0, C-v_{i}-w_{i}=0, \beta=\hat{X}^{T}W=\sum_{i=1}^{n}w_{i}x_{i}y_{i}$
Complementary:$v_{i}\delta_{i}=0, w_{i}(1-\delta_{i}-y_{i}(x_{i}^{T}\beta+\beta_{0}))$
对于对偶问题来说,SMO算法每次选择两个不满足complementary条件的$w_{i}$和$w_{j}$进行coordinate descent更新。如果每次只对一个$w_{i}$进行更新,其他固定为常数,此时由于等式约束条件$∑{i=1}^{n} w{i} y_{i} =0$的存在,使得$w_{i}$的更新值只能为
\[w_iy_i = -\sum_{k \neq i}^n w_ky_k\]SMO启发式的选择两个block $w_{1}$和$w_{2}$同时更新,此时有
\[w_1=\left( -\sum_{k=3}w_ky_k - w_2y_2 \right) \frac{1}{y_1} = (\pi - w_2y_2) \frac{1}{y_1} \\ \rightarrow w_2y_2 + w_1y_1 = \pi\]此时构造出来了一个取值域(图里的$a$就是我们的$w$),这个可行域由上式的等式与w本身的取值范围组成,最后组成了一条正方形中的线段。
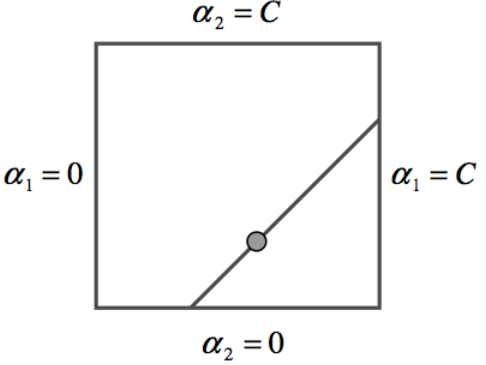
此时把$w_1$的形式带回到对偶形式中,得到关于$w_2$,在一定取值范围内的二次问题,而这个取值范围由上图的线段投影到$w_2$方向上的范围决定。同理得到$w_1$的更新值,从而完成一次coordinate descent的迭代
0x04_3 Conditional Gradient Method
考虑优化问题 $\min_{x} f(x) \quad s.t. x\in C$,其中$f$是光滑凸函数,$C$是凸集。这个问题可以采用projected gradient descent算法进行求解,这个算法是在普通gradient descent方法上,再加了一个projection操作,保证解的可行性。具体来说它首先由一个初始点$x^{0}$出发,进行下式的迭代,其中$P_{C}$表示投影到凸集$C$上的一个projection操作
\[x^k=P_C \left( x^{k-1} - t_k \triangledown f(x^{k-1}) \right)\]这个过程可以转化为对$f$的二次泰勒展开,进一步的泛化成下式的迭代式子
\[x^k=P_C \left( \arg\min_y \triangledown f(x^{k-1}) ^T (y-x^{k-1}) + \frac{1}{2t} \| y - x^{k-1} \|_2^2 \right)\]而conditional gradient method(或者叫Frank-Wolfe Method)采用的也是对$f$的局部的线性展开的性质,其展开的形式如下,其中$S$表示常数。
\[f^{linear}(s) = f(x^{k-1}) + \triangledown f(x^{k-1})^T (s-x^{k-1}) \\ =\triangledown f(x^{k-1})^T s + S\]Conditional gradient通过最小化这个线性近似来找下一个迭代点,可以看到,如果问题本身是无约束优化问题,那么$f^{linear} (s)$的最小值就是负无穷,所以conditional gradient并不适用于无约束优化问题。此时他的迭代式子为
\[s^{k-1} \in \arg\min_{s \in C} \triangledown f(x^{k-1})^T s \\ x^k = (1-\gamma_k) x^{k-1} + \gamma_k s^{k-1} = x^{k-1} + \gamma_k (s^{k-1} - x^{k-1})\]其中,步长设置范围为0到1,默认步长大小为$γ_{k}=2/(k+1)$。如下图所示,当前点在$x$出,$D$是可行域,函数$f$为蓝色部分,在$x$点出的线性近似为红色平面,此时,线性近似的最小值在$S$点处取得,下次的更新方向是$x$向$S$移动。可以看出算法的精确性受到了函数$f$本身的线性性的制约,如果$f$并不太具有线性性,那么用线性近似的方法获得的更新方向是不准确的。并且,随着迭代次数的增加,步骤不断地减小,最小化线性函数的方向$s^{k-1}$的作用越来越小,此时上面提到的不准确性效果也渐渐减小。一般来说对于很多问题而言,这种通过在凸集$C$上求线性近似最小化的方法会比一般基于凸集$C$的投影的方法,要简单高效很多。但是该方法却并不是一个descent method
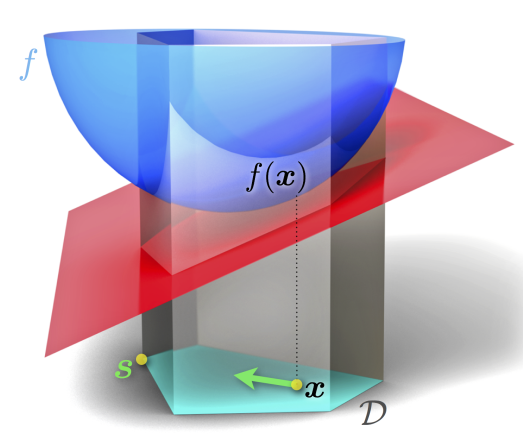
算法步骤如下

如果问题的约束条件是一个norm,即$C={x:‖x‖≤t}$,此时函数的线性近似的最小值的约束条件变成了$‖x‖≤t$,即
\[s^{k-1} \in \arg\min_{ \|s\| \le t} \triangledown f(x^{k-1})^T s\]令$s=At$,则有
\[s^{k-1} \in \arg\min_{ \|At\| \le t} \triangledown f(x^{k-1})^T At\\ = -t \left( \arg\max_{ \|A\| \le 1} \triangledown f(x^{k-1})^T A\right)\]根据对偶部分提到的dual norm的定义,可以把上式进一步简化为下式,其中$‖x‖_{*}$是$‖x‖$的dual norm,所以问题转换为求dual norm $‖∇f(x^{k-1})‖_{*}$ 的subgradient,只要知道了它的表达式,conditional gradient就能快速求解,快过proximal operator
下面用具体的L1 norm的例子来进一步说明。给定Lasso优化问题
\[\min_x f(x) \\ s.t. \|x\| \le t\]由于L1 norm的dual norm是无穷范数 $‖.‖_{∞}$,所以此时线性近似的最小值更新方向为
\[s^{k-1} \in -t \partial\| \triangledown f(x^{k-1})\|_{\infty}\]对于任意一个$m$维的向量$b$来说,他的无穷范数$‖b‖_{∞}=\max(abs(b_{1}),abs(b_{2}),…, abs(b_{m}))$,假设第$i$维取得最大,此时他的subgradient为$sign(abs(b_{i}))$,所以,令$e_{i}$表示第$i$维为1,其他维度为0的向量,这个问题的更新方式为下式,其中$sign(b_{i}) e_{i} \in \partial | b|_{\infty}$
\[i_{k-1} \in \arg\min abs(\triangledown_i f(x^{k-1}))\\ x^k = (1-\gamma_k)x^{k-1} - t \gamma_k sign\left( \triangledown_{i_{k-1}} f(x^{k-1}) \right) e_{i_{k-1}}\]这时候,可以看做是从每个维度中选择一个方向,这个方向能使得函数值下降最快,类似于贪心的coordinate descent。而下图给出的是该方法与proximal方法的比较,注意这里的conditional方法采用的是固定步长的方式,但是实际上,conditional方式也难以获取高精度的解