历史笔记迁移系列

Word转markdown真的好累

第二集：优化算法の笔记（中） - Duality Method & Second Order Methods

第三集：优化算法の笔记（下） - ADMM & Coordinate Descent

0x00. 说在前面的话

0x00_1. Convex Optimization Programming

凸优化问题定义为下面这个形式

\[\min_{x \in D} f(x) \\ s.t. g_i(x) \le 0, i=1,2,...,m\\ Ax=b\]

其中：

$f(x)$是我们要最小化的目标函数，一般使用$x^{*} $表示最优解（Optimal Value）
$D$表示Optimization Domain，一般这不会明显的直接给出来，但可以表示成$D=domain(f) \cap domain(g_{i})$。在$D$中，并且满足约束条件的点叫做可行点（feasible point）
$g_{i}$表示不等式约束（inequality constraints），他是一个凸函数。如果存在一个$x_{0}$，使得$g_{i}(x_{0})=0$，那么称$g_{i}$是Active的。
$X_{opt}$是解（solution）的集合，并且是一个凸集（convex set）。如果$X_{opt}$中只有一个元素，则称为Unique solution
$\epsilon-suboptimal$是指一个满足$f(x) \le f^{*}+\epsilon$的可行点$x$
局部最优和全局最优（Locally / Global Optimal）的区别在于，一个可行点是否在一个局部的领域里能取到solution。比如，存在一个$R>0$，使得$f(x)\le f(y)$对所有满足$\parallel x-y \parallel_{2} \le R $的$y$都成立。对于全局最优来说，他的solution是在整个optimization domain上。对于凸优化来说，局部最优就是全局最优。
如果$f(x)$是严格凸的（即对于任意$x \neq y$和$t\in(0,1)$来说，满足$f(tx+(1-t)y)<tf(x) + (1-t) f(y)$ ），那么他的solution是唯一的。假设solution不唯一，存在$x\neq y$，使得$f(x)=f(y)=f^{*}$，那么可以推出$f(tx + (1-t)y) < tf^{*} + (1-t)f^{*}=f^{*}$，即$f^{*}$不是最优解。所以solution一定是唯一的。

0x00_2. Partial Optimization

给定$f$在变量$(x, y)$上是convex的，并且$C$也是凸集，那么，$g(x)=\min_{y \in C}⁡ f(x,y)$在$x$上也是convex的。因此我们常常对一个凸问题进行局部优化以保证他的凸性(retain convexity)，这也是坐标下降等算法的理论动机。即，如果下面这个原始凸问题可以对原始变量$x$进行分解（decompose）成$x=(x_{1},x_{2})$

\[\min_{x_1,x2} f(x_1,x_2)\\ s.t. g_1(x_1) \le 0, g_2(x_2) \le 0\]

那么，下面这个问题也是凸的

\[\min_{x_1} \widetilde{f}(x_1)\\ s.t. g_1(x_1) \le 0, \widetilde{f}(x_1)=min\{f(x_1,x_2): g_2(x_2) \le 0\}\]

0x00_3. Formation

凸优化是优化问题中的一大类，下图给出了各种子问题的层次结构，其中包括线性规划（LP, Linear Programming），二次规划（QP, Quadratic Programming），二阶锥规划（SOCP, Second-order Cone Programming）和半定规划（SDP, Semi-definite Programming）

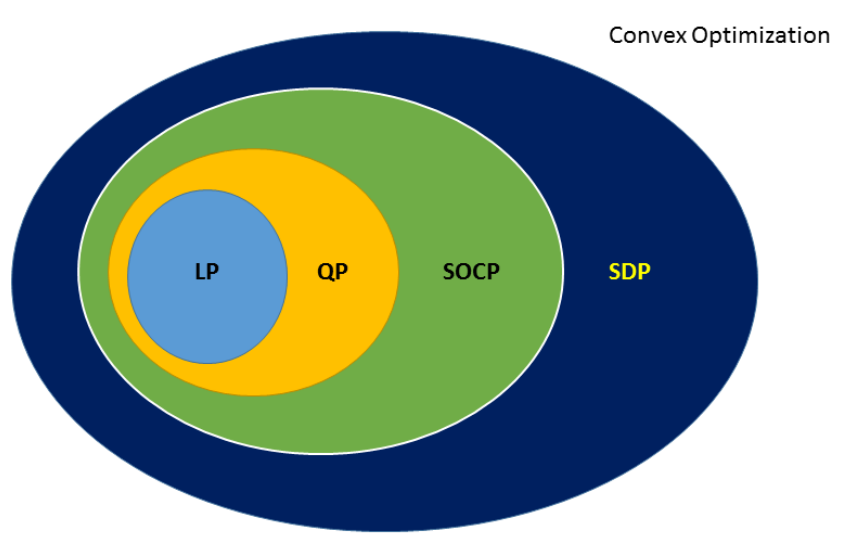
下面是各类问题的定义

类型	形式	说明
LR
QP		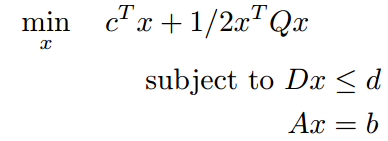Q是对称半正定矩阵。也只有Q是半正定的时候，才是凸问题
SDP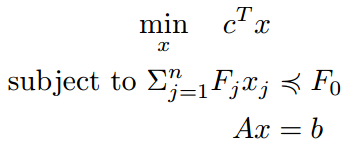
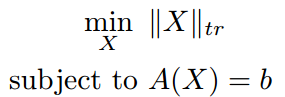SOCP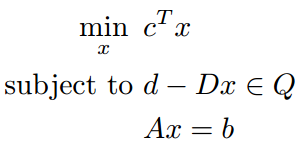

0x01 First-order Methods

0x01_1 Gradient Descent

梯度下降，无约束优化中的常用方法，假设函数$f(x)$是可微的光滑凸函数，满足$domain(f)=R^{n}$，下式的优化目标形式成为无约束优化

\[\min f(x)\]

为了求解出这个 $ x^{*} $，我们可以直接求解$\bigtriangledown f(x^{*} )=0$，但是不容易直接求解出来的。然后我们可以采用迭代的方式，找出一组$x$的序列$x^{0}, x^{1},$满足当$k \rightarrow \infty$时，$f(x^{k}) \rightarrow f(x^{*})$。梯度下降便是这样的迭代算法，给定初始$x^{0}$，该算法的$x$序列设置为

\[x^k = x^{k-1} - t_k \nabla f(x^{k-1})\]

其中，$k$是迭代次数，$t_{k}>0$是每次迭代的步长，这样的更新方式可以保证每次迭代之后的函数值都有所减小，即通过泰勒展开，以下式子成立

\[f(x^k) = f(x^{k-1} - t_k \nabla f(x^{k-1})) \\ \approx f(x^{k-1}) - t_k \nabla f(x^{k-1})^T f(x^{k-1}) \\ \le f(x^{k-1})\]

需要注意的是，梯度下降算法可能会收敛到局部最优解，这取决于目标函数是否是convex的

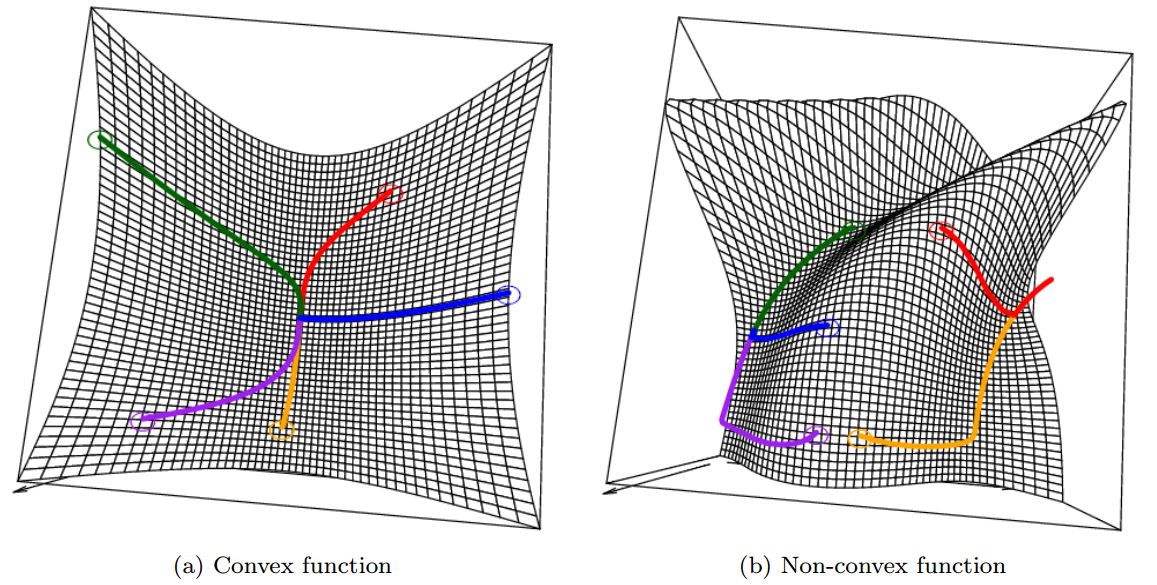
下面来看看梯度下降的更新式子是怎么来的。一般来说，有两种视角。

视角1：假设函数$f$是二阶可微的，那么用泰勒公式进行展开，其中，$1\le \theta \le 1$

\[f(y)≈f(x)+∇f(x)^T (y-x)+\frac{1}{2} (y-x)^T ∇^2 f(θ(x-y)+y)(y-x)\]

现在对$∇^{2} f(θ(x-y)+y)$用$\frac{1}{t}I$进行二级近似，那么得到

\[f(y)≈f(x)+∇f(x)^T (y-x)+\frac{1}{2t} \parallel y-x \parallel_2^2=g(y)\]

为了使得函数值在每次迭代中降低，所以需要$y$的值，使得$∇g(y)=0$，等价于$∇f(x) +\frac{1}{t} (y-x)=0 \leftrightarrow y=x-t∇f(x)$

视角2：考虑泰勒展开$f(y) \approx f(x) + \bigtriangledown f(x)^{T}(y-x)$，记$(y-x)=ad_{k}$，$a$是给定的一个数。若$∇f(x)^{T} d_{k}<0$，这方向$d_{k}$则是我们要的使得函数值下降的方向。另外，结合Cauchy-Schwartz不等式，得到

\[\| \bigtriangledown f(x)^T d_k \| \le \| \bigtriangledown f(x)^T \| \| d_k \|\]

所以当且仅当$d_{k}=-∇f(x)^{T}$时，函数值下降得最快，所以负梯度方向是最速下降方向。

梯度下降中，我们是沿着负梯度的方向进行迭代更新，但是每次更新的步长选择也很重要。步长控制着前后两次取点的大小，如果步长太大，算法可能不会收敛，而产生很大的震荡，如果步长太小，则算法收敛的时间将变得很慢，如下图所示。所以如何选择合适的步长，在实际使用中至关重要，下面介绍两种方式：Backtracking line search和Exact line search

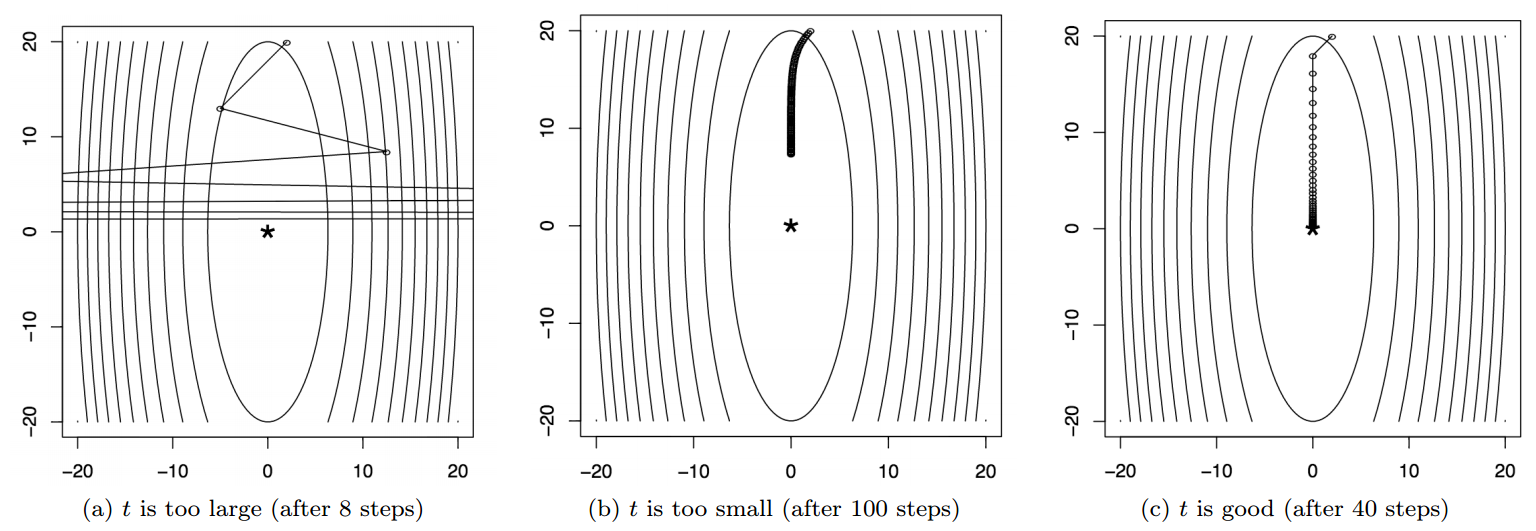
Exact line search：在实际编程使用中并不太常用，因为他对步长还求了一次最小，使得函数值进一步降低。但是这个步骤还不如一般的BLS的方法高效，但是他比较适用于教学与考试。Backtracking line search（BLS）：旨在更新的过程中缩小步长，控制步长变得太大

当步长t足够小的时候，他应该会满足下式

\[f(x-t∇f(x))≈(f(x)-t \parallel ∇f(x)\parallel_2^2 )<f(x)-at‖∇f(x)‖_2^2\]

所以当步长太大时，BLS算法会缩短步骤，否则就选取下一个迭代点。下图是BLS对比一般梯度下降的结果图，上图原函数，下图为每次迭代后的函数值，GD采用固定步长t=0.9（这里t=1的话，不会收敛），BLS的步长初始化为t=1，两个参数$a$,$β$都设为0.5

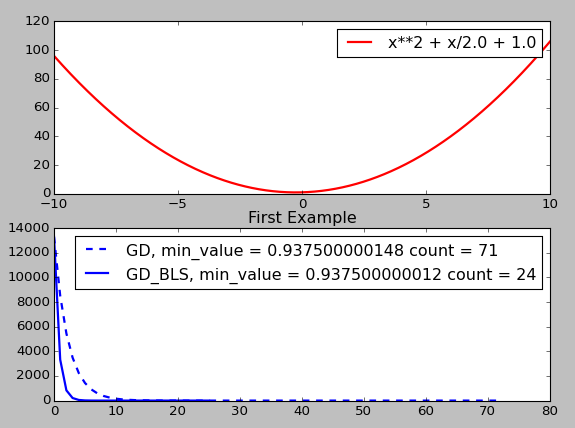
0x01_2. Subgradient Method

梯度下降虽然简单实用，但是遇到不可微的函数，那就捉襟见肘了。事实上在这种情况下，还有次梯度Subgradient的存在。我们说一个函数$f(x)$是凸函数，则他的一阶充要条件是函数$f$可行域是凸集，并且在可行域中的任意点都满足$f(y) \ge f(x) + \bigtriangledown f^{T} (x) (y-x)$。即对于一个凸函数来说，其一阶泰勒近似实质上是原函数的一个全局下估计，subgradient的定义与这个很相似，一个凸函数$f$在点$x$处的subgradient定义为，满足以下条件的任意$g \in R^{n}$

\[f(y) \ge f(x) + \bigtriangledown g^T (y-x) , \forall y\]

记$∂f(x)$表示在点$x$处，函数f的subgradient能取到的所有值的集合，值得一提的是$∂f(x)$也是闭的凸集。另外，如果函数$f$在$x$点处可微，那么这点的subgradient就是这点的gradient，否则，subgradient仍然存在，即无论什么情况，subgradient都希望达到全局下估计。另外对于不是convex的函数，subgradient也是可能存在的。下面给出几个subgradient的例子

原函数	次梯度
$f(x)=abs(x)$	当$x \neq 0$，次梯度是$sign(x)$，否则取$[-1,1]$中的任意值
二范数$\|x\|_2$	当$x \neq 0$，次梯度是$\frac{x}{\|x\|_2}$，否则满足$\|g\|_2 \le 1$的任意$g$都是次梯度
一范数$\|x\|_1$	当第$i$维的梯度向量$g_{i} \neq 0$，次梯度是$sign(x_{i})$，否则满足$[-1,1]$的任意值都是该维度的次梯度值
$L_{P}$范数	$\|x\|_{q}$，满足$\frac{1}{p} + \frac{1}{q} = 1$

引入subgradient之后，我们可以吧gradient视为subgradient的一个特殊情况，那么进一步可以得到下面的优化条件（subgradient optimality condition），即如果$x$*是最优解，当且仅当在$x$*处的subgradient的集合包含0

\[f(x^*) = \min_{x} f(x) \leftrightarrow 0 \in \partial f(x^*)\]

此时，对任意的$y$，都有$f(y) \ge f(x*) + 0^{T}(y-x)$成立。并且，对于有约束的优化问题来说，上面的优化条件也同样成立。那么，是否能用subgradient代替gradient descent中的gradient，就可以得到subgradient methods呢？可以，但是这两者之间还是有区别，因为一个凸函数在某一点的subgradient可以有很多，subgradient method的更新规则是选择任意的一个就行，即：

\[x^k = x^{k-1} - t_k g^{k-1}, g^{k-1} \in \partial f(x^{k-1})\]

也正因为如此，subgradient method也不一定是一个decent的方法，即negative subgradient方向可能不是一个下降方向！如下图所示：（-1，-2）是一个negative subgradient方向，但是他明显不是个下降方向

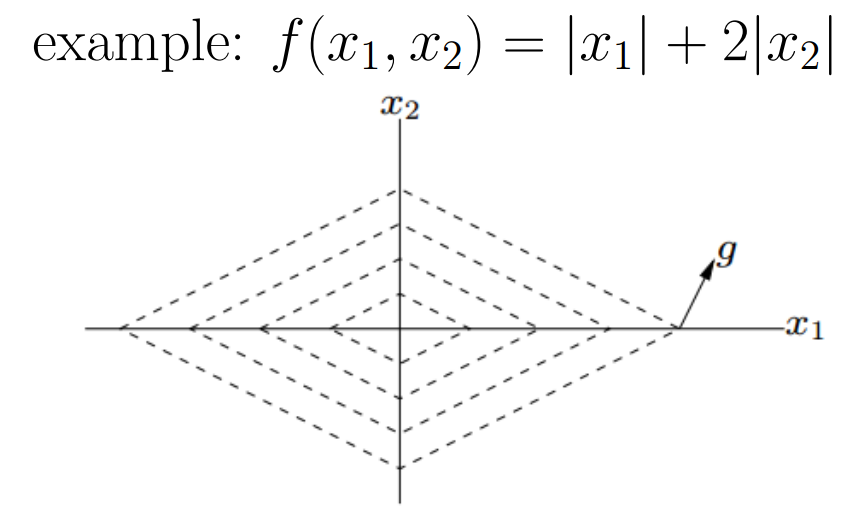
另外，和gradient descent一样，subgradient method的步长的选择也很困难，而且并没有像backtracking一样的方法存在，对于subgradient method来说大体上有两种步长选择方式：

固定步长t
逐渐降低步长（diminishing step sizes），但是步长的消散不能太快，避免多次迭代后，步长变成0，即要满足下面的两个条件。一个步长选择的例子就是$t=\frac{1}{k}$

\[\sum_{k=1}^{\infty} t_k = \infty \\ \sum_{k=1}^{\infty} t_k^2 < \infty\]

在logistic regression + lasso的条件下，通过两种选择步长的方式，可以得到下图

讲了这么多，下面给出一个用subgradient求解的例子，考虑一个Lasso优化问题

\[\min_\beta f(x) = \frac{1}{2} \| y-X\beta\|^2_2 + \lambda \|\beta\|_1, (\lambda \ge 0)\]

来吧，次梯度下降，我们对$f(x)$里的$\beta$求次梯度：

\[\partial f(x) = \partial (\frac{1}{2} \| y-X\beta\|^2_2 + \lambda \|\beta\|_1) = -X^T(y-X\beta) + \lambda \partial \|\beta\|_1 = 0\\ \rightarrow X^T(y-X\beta) = \lambda \partial \|\beta\|_1 \\ \beta的次梯度：\partial \|\beta\|_1 = \left\{\begin{matrix} 1 \quad if \quad\beta_i > 0 \\ -1\quad if \quad \beta_i < 0 \\ [-1,1]\quad if \quad \beta_i = 0 \end{matrix}\right.\]

综合起来就可以得到下式

\[\left\{\begin{matrix} X_i^T(y-X\beta) = \lambda sign(\beta_i) \quad if \quad \beta_i \neq 0 \\ |X_i^T(y-X\beta)| \le \lambda \quad if \quad \beta_i = 0 \end{matrix}\right.\]

通过上式可以把$\beta$给解出来，现在我们把问题再简化一下，考虑$X=I$的情况，方便我们求解，此时，上面的式子简化为

\[\left\{\begin{matrix} (y-\beta) = \lambda sign(\beta_i) \quad if \quad \beta_i \neq 0 \\ |(y-\beta)| \le \lambda \quad if \quad \beta_i = 0 \end{matrix}\right.\]

可以得到$\beta_{i}$的解（这个形式在凸优化中称为soft-thresholding operator $S_{\lambda} (y)$）

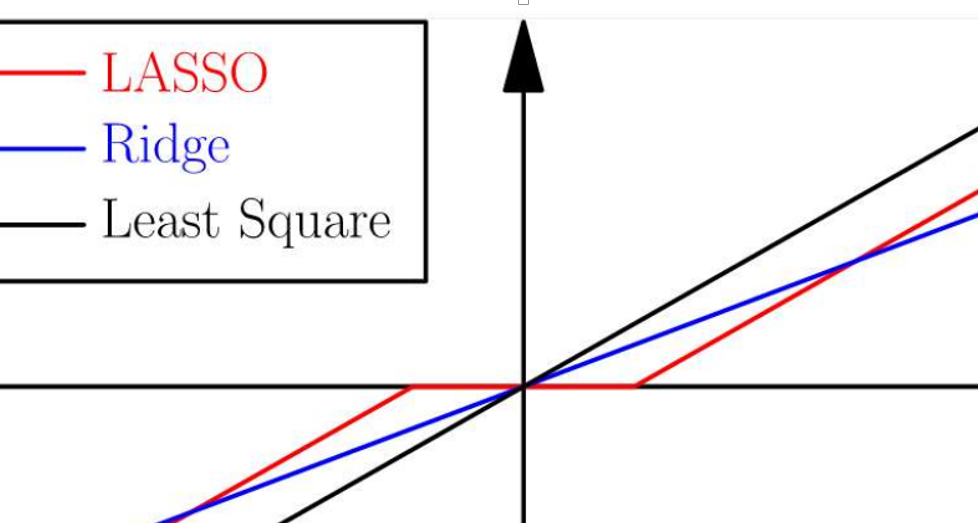
\[\beta_i = [S_{\lambda}(y)]_i = \left\{\begin{matrix} y_i - \lambda \quad if \quad y_i > \lambda \\ 0 \quad if \quad -\lambda \le y_i \le \lambda \\ y_i + \lambda \quad if \quad y_i < - \lambda \end{matrix}\right.\]

这个式子就可以看出很多东西，回想在机器学习中，我们常说Lasso用来获取稀疏解，是L0范数的最优凸近似。其实Ridge和Lasso在统计学中，都是对系数做收缩的方法，可以Lasso却可以很奇妙的把系数收缩到0，从而相当于做了系数选择，得到了稀疏的解。神奇的事发生了，在我们这种问题简化的版本下，当$-\lambda \le y_{i} \le \lambda $的时候，参数$\beta_{i}$被置为了0，起到了稀疏化的功能。当然，当$X \neq 1$的时候，这个解的条件还与$X$的取值有关。由此就可以得到这一副经典的图片

0x01_3. Stochastic Subgradient Method and Batch Method

SGD & mini-batch

Stochastic method在处理加法模型的时候帮助很大，即目标函数是大量的子函数的加和的情况。这是在求机器学习的经验风险的时候经常遇到的情况，即考虑$\min \sum_{i=1}^{m} f_{i}(x)$，当m的值很大，或者说，数据量很大的时候（此时，相当于的经验风险函数中含有很多子函数），此时使用subgradient method（或者gradient descent），对应下式，m很大的话，这计算量是很恐怖的

\[x^k = x^{k-1} - t_k \sum_{i=1}^m g_i^{k-1}, \quad where \quad g_i^{k-1} \in \partial f_i(x^{k-1})\]

Stochastic method的在于把上式变成下式，即在第k次迭代中，只使用一个子函数的subgradient进行更新，以经验损失的角度来看，就是每次迭代只计算一个数据的subgradient进行更新，这样做大大的加快了速度，减少计算量。

\[x^k = x^{k-1} - t_k g_{in}^{k-1}, \quad where \quad {in} \in \{1,2,...,m\}\]

$g_{i}^{k-1}$的选择也有两种方式，一种是随机的从$m$中选择一个，另一种是循环依次的使用各个子函数的subgradient。当然除了Stochastic method外，还有一个在准确性，稳定性和$m$之间更折中的方法，batch method，即

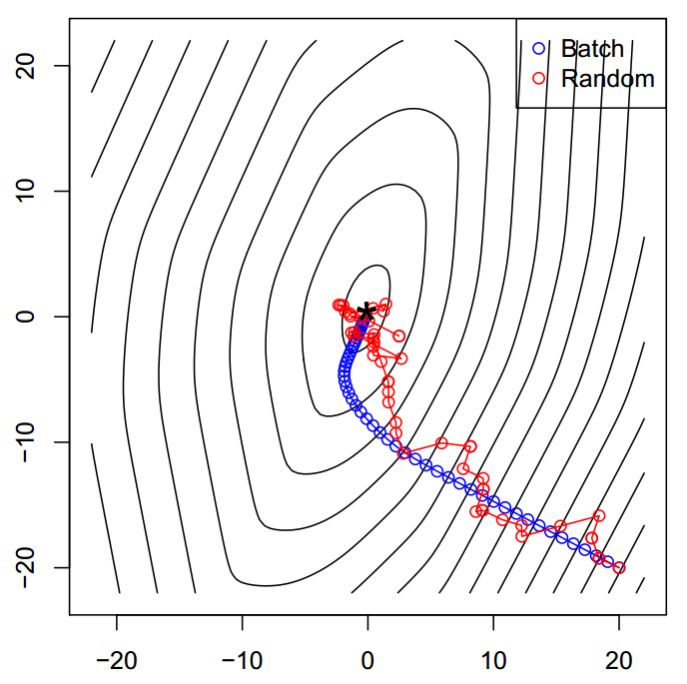
\[x^k = x^{k-1} - t_k \sum_{i=1}^{m_{batch}} g_i^{k-1}\]

batch method旨在一次更新的时候，选取一部分的子函数用来更新（或者说，使用一部分数据来更新）。两者之间的区别在于$m_{batch}$次stochastic更新，近似等于一次batch更新，这里假设他们所选的更新子函数集都是相同的

\[x^{k+m_{batch}} = x^k - t \sum_{i=1}^{m_{batch}} \triangledown f_i(x^{k+i+1}) \quad m_{batch}\_time\_stochastic\_update\\ x^{k+m_{batch}} = x^k - t\sum_{i=1}^{m_{batch}} \triangledown f_i(x^k) - t\sum_{i=1}^{m_{batch}} (\triangledown f_i(x^{k+i+1}) - \triangledown f_i(x^k))\]

这里有张两者之间的效果对比图，可以感受一下。另外，SGD要想train得好，也有一些经验方法可以参考

Shuffling ：旨在打乱做SGD时候的样本顺序，一般每一轮之后打乱一次。取得更好的收敛性，也有助于避免local minimal
Batch Norm：一般采用零平均值和单位方差的方法来归一化参数，可以加快收敛
Early stopping：分出一个验证集，每过一定迭代轮数就看下验证集上的error是否有变化，如果没有变化或者出现上升则停止迭代
Gradient Noise：出淤泥而不染，在更新的梯度里适当的增加noise，挺像在强化学习里的探索策略。

站在训练数据集的角度上来说，每次更新，根据选择多少数据点来训练模型，可以把算法分为普通的Gradient descent，Batch based和stochastic based。由于stochastic gradient descent收敛并不理想，现有很多的加速算法，比如Nesterov accelerated gradient，Momentum based，Adagrad，Adadelta，RMSprop，Adam，AdaMax，Nadam。这些改进的算法要么在下降方向上做文章，要么考虑了迭代步长的自适应选择

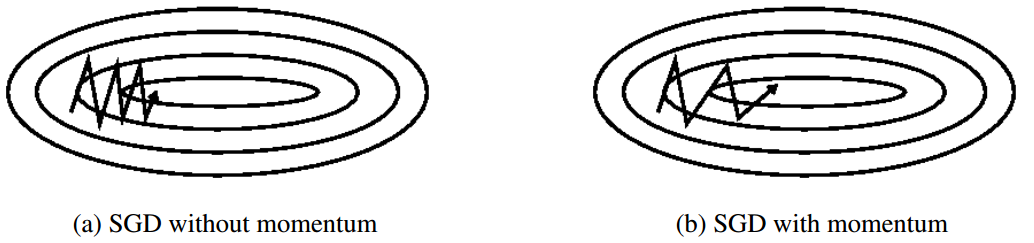
Momentum

传统的梯度下降算法的下降方向由当前的梯度负方向确定，而基于动量的方式还考虑了上一轮的迭代方向。其认为当前的更新方向是上次的更新方向与当前梯度方向的带权加和。即

\[v^k = r v^{k-1} + \mu \triangledown_\beta f(x;\beta) \\ \beta^{k} = \beta^{k-1} - v^k\]

其中，$r$控制了动量项的效果（一般取值0.5/0.9/0.99）。当然更好的方式是初始化$r$为一个比较小的数，然后随着迭代次数不断的增加

Nesterov Accelerated Gradient

该方法是在momentum的基础上，先沿着上一轮的动量方向走一点，再做momentum更新。通过步骤$\beta - r v_{t-1}$，可以用来估计下一次参数的值。起到一个”look ahead”的作用。并且由下图，可以看出NAG的更新方向更靠近真实的梯度方向，使得NAG的收敛速度比动量的方式更快。（但是在随机梯度下降的框架下，并没有改进）

\[v^k = r v^{k-1} + \mu \triangledown_\beta f(x;\beta - r v_{t-1})\\ \beta^{k} = \beta^{k-1} - v^k\]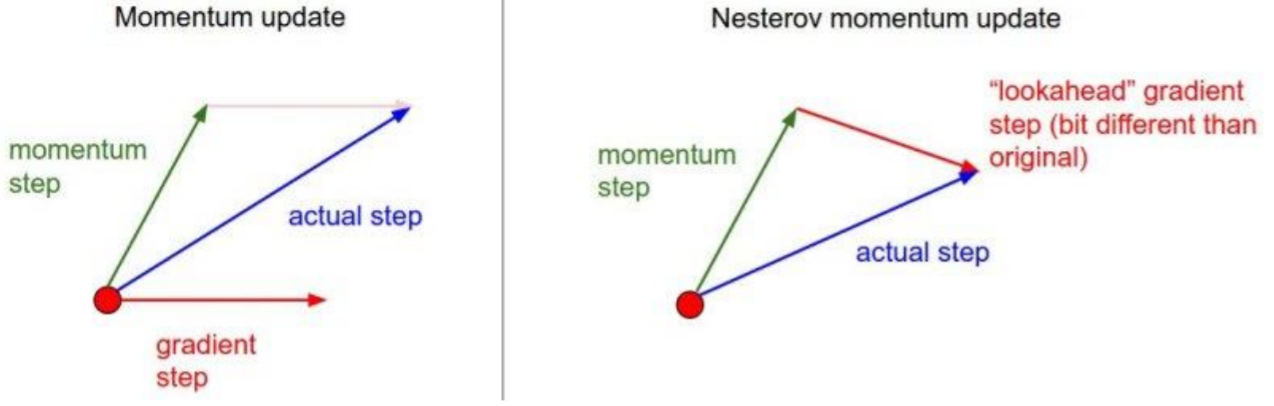

Adagrad

Adagrad能自适应选择更新步长，并且能更细腻的，对于参数的不同维度上有不同的步长选择，能很好的处理sparse data，保证数据充足的维度步长更小（有足够的数据来学习，就不要担心学不好，慢慢来学就行），对于难于学习的维度，有更大的步长（数据吃不饱，就不放过任何一次机会，aggressive的学呗）。对于第i维参数，他的更新式子为：

\[\beta_{t+1,i} = \beta_{t,i} - \frac{\mu}{\sqrt{G_{t,ii} + \epsilon}} g_{t,i}\]

其中$g_{t,i}$是当前梯度的第i维，$G_{t,ii}$是对角矩阵G的第i-i元素，代表从开始到第t时刻的，$\beta_{i}$的梯度的平方和，而$\epsilon$是一个防止除零的小整数（1e-8）。$\mu$一般取值0.01。然而随着迭代的进行，$G_{t,ii}$会变得越来越大，使得步长缩减太快，后面几乎学不到什么东西。

Adadelta

Adadelta是Adagrad的扩展，他通过维护一个窗口，限制$G_{t,ii}$为前$k$个梯度的平方和，削减步长衰减。但是在具体实现中没有直接只保存前$k$个梯度，而是采用了权重衰减的策略，为每一个梯度值都赋予一个加权和的权值。该算法会维护一个梯度的running average $E[g^{2}]_{t}$：(把式子展开就是每一项$g_{t}^{2}$的加权和)

\[E[g^{2}]_{t} = \gamma E[g^{2}]_{t-1} + (1-\gamma) g_t^2\]

Adam

Adam是自适应的动量算法，和Adadelta很像，也是一个在步长上做文章的算法。Adam保留了梯度的一阶矩和二阶矩信息，并且同样对这些信息做指数衰减，即

\[m_k = \lambda_1 m_{k-1} + (1-\lambda_1) g_k \\ v_k = \lambda_2 v_{k-1} + (1-\lambda_2) g_k^2 \\\]

由此可以得到类似于Adadelta的更新方式

\[\beta_{t+1} = \beta_{t} - \frac{\mu}{\sqrt{\widehat{v_t}} + \epsilon} \widehat{m_t}\\ \widehat{v_t} = \frac{v_t}{1-\lambda_2^t} \\ \widehat{m_t} = \frac{m_t}{1-\lambda_1^t} \\\]

式子里没之间用m和v，这样做的目的在去除m和v的bias（don’t know why），相当于是一个修正项。常用取值$\lambda_{2}=0.999$，$\lambda_{1}=0.9$，$\mu=0.002$

AdaMax

AdaMax是Adam是扩展版本，在adam中，$v_{t}$是集合了历史梯度的L2范数的信息，AdaMax是打算扩展到Lp范数上，尤其是${L_{\infty}}$范数的时候

0x01_4. Proximal Gradient Method

对于不可微的凸函数f，前面我们介绍的subgradient method，从收敛性的角度来说是不可观的。假设，我们想要误差精度$\epsilon=0.001$，即$f(x^{k})-f* \le \epsilon$，梯度下降要迭代$O(1000)$次，subgradient method却要用1百万迭代（关于各个算法的收敛性，将在后面章节汇总给出）！那么需要如何加速收敛呢？

现在考虑函数$f$，可以分解成两个函数的和$f(x)=g(x)+h(x)$，其中$g(x)$是可微的凸函数，$dom(g)=R^{n}$，$h(x)$是形式简单，不一定可微的凸函数。对于这样的函数$f$，可以采用proximal gradient descent的方法，保证$O(\frac{1}{\epsilon})$的收敛率。现在来看看，这个函数是怎么分解的。

我们令$f(x^{+})=g(x^{+})+h(x^{+})$，回忆Gradient descent的第一种推导，我们对函数进行一次泰勒展开，并用$\frac{1}{t}I$二次近似$\triangledown^{2}f(x)$，得到的函数的最小值就是下一步的$x^{+}$，即

\[x^+=arg\min_z f(x) + \triangledown f(x)^T(z-x) + \frac{1}{2t}\|z-x\|^2_2\]

既然$g$是可微的，则对$g$同样做的动作

\[x^+=arg\min_z g(x) + \triangledown g(x)^T(z-x) + \frac{1}{2t}\|z-x\|^2_2 + h(z)\]

由于，上式右边是关于$z$的函数，所以等价于

\[x^+=arg\min_z \frac{(t \triangledown g(x))^2}{2t} + \triangledown g(x)^T(z-x) + \frac{1}{2t}\|z-x\|^2_2 + h(z) \quad 第一项是为了配平方\\ = \frac{1}{2t} \| (z-x) + t \triangledown g(x) \|^2_2 + h(z)\\ = \frac{1}{2t} \| z - (x - t \triangledown g(x)) \|^2_2 \\ = Prox_{h,t} (x - t\triangledown g(x))\]

其中，定义proximal mapping为关于$h$和$t$的函数，即

\[Prox_{h,t}(x) = arg\min_z \frac{1}{2t} \| z-x \|^2_2 + h(z)\]

可以看出$Prox_{h,t} (x)$是与$g(x)$无关的，只有$h(x)$有关，所以，计算$Prox_{h,t} (x)$的复杂度很大程度上依赖$h(x)$。而$Prox_{h,t} (x-t \triangledown g(x))$从形式上看，这个式子的最优解$z$使得第一项逼近$g$的梯度下降值，并且需要也使得第二项变小。现在，我们就可以来说说proximal gradient descent咯。给定初始点$x^{0}$，第$k$次的迭代点为

\[x^k= Prox_{h,t_k} (x^{k-1} - t_k \triangledown g(x^{k-1}))\]

我们在引入一个例子，之前在subgradient method中提到过解Lasso的问题，现在再把这个问题转化成proximal的形式再感受感受。我们的目的是求解$\beta$

\[\min_\beta f(x) = \frac{1}{2} \| y-X\beta\|^2_2 + \lambda \|\beta\|_1, (\lambda \ge 0)\]

这里的函数就自带分解成了两个部分，那就可以带公式了

\[Prox_{h,t}(\beta) = arg\min_z \frac{1}{2t} \|z-\beta\|_2^2 + \lambda \|\beta\|_{1} \\ \leftrightarrow arg\min_z \frac{1}{2} \|z-\beta\|_2^2 + t \lambda \|\beta\|_{1} \\ = S_{\lambda t}(\beta) \quad 记上式为这符号\]

神奇的事发生了，还记得在subgradient那部分解Lasso问题的最后，我们把$X=I$，然后得到的解是Soft-thresholding operator $S_{\lambda} (y)$，只不过由$\lambda$变成了$\lambda t$，也就是说对于Lasso问题，proximal mapping的解就是Soft-thresholding operator $S_{\lambda t} (\beta)$。既然我们已经得到了解，那么接下来就可以直接求解下一步的迭代值为下式。过程上来说，是先对$g$函数走一步梯度下降，然后进行Soft-thresholding operation。

\[\beta^+ = Prox_{h,t}(x-t\triangledown g(\beta)) = S_{\lambda t}(\beta + tX^T(y-X\beta))\]

这个求解方法，就是解Lasso的著名算法Iterative soft-thresolding algorithm (ISTA)，这个算法很牛逼，与之前用subgradient method的方法解Lasso相比，收敛快了很多，如下图

另外Backtracking Line Search也是同样适用于proximal method的！不过不在$f$上直接做文章，而换成$g$。也就是说当满足下式的时候，进行步长收缩，否则更新$x^{k+1}$：

\[g(x-t G_t(x)) > g(x) - t\triangledown g(x)^T G_t(x) + \frac{t}{2} \|G_t(x)\|^2_2\\ where \quad G_t(x) = \frac{x - Prox_{h,t}(x-t\triangledown g(x))}{t}\]

下面我们来看一些例子：

当$h(x) = 0$时，proximal gradient descent就是Gradient Descent
当$g(x)=0$时，proximal gradient descent就是proximal minimization algorithm
当h(x) 是indicator function，那proximal gradient descent就是Projected Gradient Descent

projected gradient descent

indicator function是指在定义域中取值为0，否则为无穷，用于限制一定的可行域的函数

\[\min_{x\in R^n} g(x) + I_C(x) \leftrightarrow \min_{x\in C} g(x) \\ where \quad I_C(x) = \left\{\begin{matrix} 0 \quad if \quad x \in C \\ \infty \quad otherwise \end{matrix}\right.\]

这个时候我们可以写出Prox函数

\[Prox_t(x) = arg\min_{z \in R^n} \frac{1}{2t} \|x-z \|^2_2 + I_C(z) \\ =arg\min_{z \in C} \frac{1}{2t} \|x-z \|^2_2\]

所以更新公式变成了下式，这里的$P_{C}(x)$是distance to a convex set的问题，最优值就是x在C上的投影，所以算法称为projected gradient。即先不管可行域，正常走梯度下降，然后将梯度下降后的值再映射到可行域边界上。

\[x^+ = P_C(x-t\triangledown g(x))\]

proximal minimization algorithm

当$g(x)=0$的时候，问题转化为，$\min h(x)$

$x^+ = Prox_t(x) = arg\min_z \frac{1}{2t} \|x-z\|^2_2 + h(z)$ 这个问题，除非我们知道$h(z)$和$Prox_{t} (x)$的close-form，不然是无法编程实现的。总的来说，基于proximal gradient的方法有一个弊端，就是$Prox_{t} (x)$的计算问题，有可能会很难解

0x01_5. Accelerated Proximal Gradient Method

该方法来自Beck and Teboulle (2008)的工作，是对Nesterov工作的扩展，旨在达到一个更好的收敛率（$o(\frac{1}{\sqrt{\epsilon}})$），给定凸函数g(x)是可微的, h(x)是凸函数，优化目标和之前一样，假设了函数$f(x)$可以分解成两部分$g(x)+h(x)$。这个算法的迭代式子如下所示，感觉像是在Proximal Gradient Descent的基础上，加上了动量的方法。

\[v=x^{k-1} + \frac{k-1}{k+1} (x^{k-1} -x^{k-2} ) \\ x^{k} = Prox_{t_k} (v - t_k \triangledown g(v))\]

为啥会是这样更新呢？略，因为我也没看论文。下面是一些汇总知识点

当$k=1$的时候，$v=x^0$，相当于执行普通的Proximal Gradient
当$k \ge 2$时，$v$相当于在$x^{k-1}$的基础上，增加了上一次的加速信息（迭代方向信息），在随着$k$增加，越来越趋于最值，gradient/subgradient越来越小，$\frac{k-2}{k+1}$的值增加，并趋于1，方向的加速信息的权重越大，加速向最值的方向收敛。
$\frac{k-2}{k+1}$的形式，与算法的收敛性有关，我也不知道为啥是这个值
当$h(x)=0$，这个方法就是Accelerated Gradient Descent

\[v=x^{k-1} + \frac{k-1}{k+1} (x^{k-1} -x^{k-2} ) \\ x^{k} = v - t_k \triangledown g(v)\]

下图是对lasso问题求解的结果（也就是对应的subgradient for lasso, ISTA和FISTA算法），可以看到这个算法简直是快啊，但是他也不能保证在次梯度上的下降性哦

0x01_6. Conclusion of Convergence Analysis

前文提到了好多算法收敛率，这部分总结了一些算法的收敛性结论，方便大家参考。首先定义一个Lipschitz continuous的概念：如果一个$f$对于定义域里的任意$x$和$y$都满足下式，则称$f$是Lipschitz连续的，满足条件的最小数$G$叫做Lipschitz常数。这个式子约束了在定义域范围内的任意两个点之间的连线，其斜率一定要是有界的，所以变动$f(x)$中$x$的取值，函数值不会存在大幅度的突变。

\[\|f(x) - f(y) \| \le G \|x-y\|_2\]

另外我们还需要定义另一个概念，强凸函数（strongly convex）。给定$m>0$，如果函数$f(x)-\frac{m}{2} | x|_{2}^{2}$是凸函数，那么函数$f(x)$是强凸的。现在，假设下面结论中的凸函数$f$是可微的，并且$dom f=R^{n}$，Lipschitz常数为$L>0$。

Gradient Descent的收敛性

对于固定迭代步长$t$，并且$t \le \frac{1}{L}$，他的收敛率是$o(\frac{1}{k})$，换句话说，如果要想满足$f(x^{k}) - f^* \le \epsilon$，我们需要$o(\frac{1}{\epsilon})$次的迭代。

\[f(x^k) - f^* \le \frac{\|x^0 - x^* \|_2^2}{2tk}\]

如果函数$f$是强凸的，步长$t\le \frac{2}{L+m}$，那么上面的式子可以进一步的写成

\[f(x^k) - f^* \le \frac{c^kL}{2}\|x^0 - x^* \|_2^2 \quad where \quad 0<c<1\]

可以看到，这时候变成了指数级的收敛$o(c^{k})$，这个$c$依赖于$L/m$，（这个$L/m$叫做condition number，是在数值计算中的容易程度的衡量，一个低条件数的问题称为良置的，而高条件数的问题称为病态，此时收敛率相对降低），我们需要$o(log⁡(1/\epsilon))$次迭代。

如果采用了Backtracking Line Search的方式来做步长选择，那可以得到下式的收敛性，其中$\beta$是步长的收缩率，当$\beta=1$的时候，收敛率和固定步长一样

\[f(x^k) - f^* \le \frac{\|x^0 - x^* \|_2^2}{2k \min(1, \beta/L)}\]

Subgradient Descent的收敛性

对于固定步长t，满足下式。可以看出在无限次迭代之后，最优解也是得不到的，当然小的步长$t$可以缩小与最优解之间的差异

\[\lim_{k \rightarrow \infty } f(x_{best}^k) \le f(x^*) + \frac{L^2 t}{2}\]

别的定理也指出，subgradient method如果要达到$f(x^{k} )-f^* \le \epsilon$，需要$o(\frac{1}{\epsilon ^{2}} )$次迭代.

对于diminishing step来说，满足下式，最优解是可以得到的

\[\lim_{k \rightarrow \infty } f(x_{best}^k) = f(x^*)\]

Stochastic Method的收敛性

对于固定步长t，满足下式，其中，$f=\sum_{i}^{m} f_{i}$

\[\lim_{k \rightarrow \infty } f(x_{best}^k) \le f(x^*) + \frac{5(mL)^2t}{2}\]

对于diminishing step来说，满足下式

\[\lim_{k \rightarrow \infty } f(x_{best}^k) = f(x^*)\]

Proximal Gradient Descent的收敛性

若$\triangledown g$的Lipschitz常数是L>0，则：

对于固定步长$t\le 1/L$，满足下式。即收敛率是$o(1/k)$或者$o(1/\epsilon)$

\[f(x^k) - f^* \le \frac{\|x^0 - x^* \|_2^2}{2kt}\]

如果采用了Backtracking Line Search的方式来做步长选择，那可以得到下式的收敛性，其中$\beta$是步长的收缩率

\[f(x^k) - f^* \le \frac{\|x^0 - x^* \|_2^2}{2k \min(1, \beta/L)}\]

Accelerated Proximal Gradient Descent的收敛性

若$\triangledown g$的Lipschitz常数是L>0，则：

对于固定步长$t\le 1/L$，满足下式。即收敛率是$o(1/\sqrt{\epsilon})$

\[f(x^k) - f^* \le \frac{2\|x^0 - x^* \|_2^2}{t(k+1)^2}\]

如果采用了Backtracking Line Search的方式来做步长选择，那可以得到下式的收敛性，其中$\beta$是步长的收缩率

\[f(x^k) - f^* \le \frac{2\|x^0 - x^* \|_2^2}{(k+1)^2 \min(1, \beta/L)}\]

0x01_7. Parallelizing & Distributed SGD

前面都讲了SGD，那自然会联想到分布式机器学习里的SGD-style的优化算法，有机会可以单独写一个博文专门讲讲分布式机器学习，这里我们先简单提一提SGD-style的优化算法。一般来说，大概分成两类：同步更新和异步更新。

HogWild!

没记错的话，这个应该是NIPS上的文章（不算真的分布式，算是多线程），它用Lock-free的方式来异步更新参数，由于是lock-free，可能出现参数更新的override，所以他适用于sparse的参数更新，不然有冲突。比如稀疏SVM，matrix completion, Graph cut

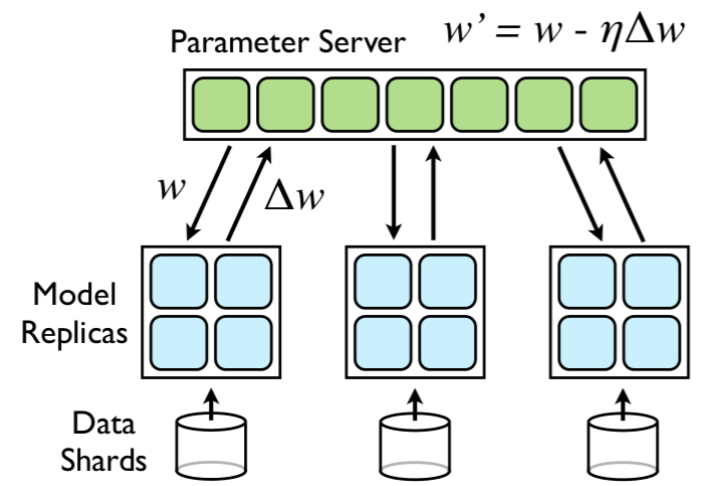
Downpour SGD

这是个基于parameter server的异步更新算法

Delay-tolerant

该算法是AdaGrad的扩展，所以能自适应的调节步长

Elastic Averaging

还是一个基于Parameter Server的可以做同步，也可以做异步更新策略。他会计算local参数和全局参数之间的差距，然后在梯度下降时，加上这个差距，使得local参数与全局参数更加相似

机器学习中的那些优化算法

优化算法の笔记（上）- First Order Methods