0. Dynamic System

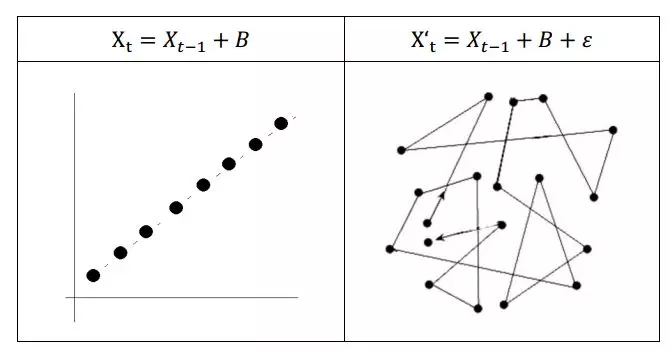
动态模型是用来描述一个给定空间（如某个物理系统的状态空间）中点随时间的变化情况。例如描述钟摆晃动、管道中水的流动，或者湖中每年春季鱼类的数量，凡此等等的数学模型都是动态系统 (From Wiki)。比如下图以点的运动为例子，左图展示了在不同时刻t上，构成的点X的移动轨迹。右图则是加入了额外噪声的情况。

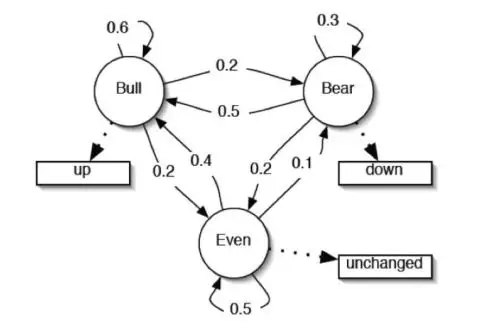
动态系统旨在对时序数据的刻画，它由三个元素组成：状态值，状态转移和观察值。比如我们以股市为例（如下的图）。它有三个状态（Bull，Bear，Even），在每个状态下股市都表现出特定的涨跌，最后每个状态之间会以一定的概率进行状态转移。

动态系统假设仅仅前后两个时刻的状态是相互依赖的，符合马尔科夫条件独立性假设。因此，可以将状态Xt看做是$X_{t−1}$的函数，$P(X_{t}\mid X_{t-1})$。而在状态$X_{t}$上，会以某种方式表现出（或被观测到）$Y_{t}$，即$P(Y_{t}\mid X_{t})$。一般来说，ML 中的动态系统可以分为三种情况，离散状态，线性高斯和非线性非高斯。如下所示：

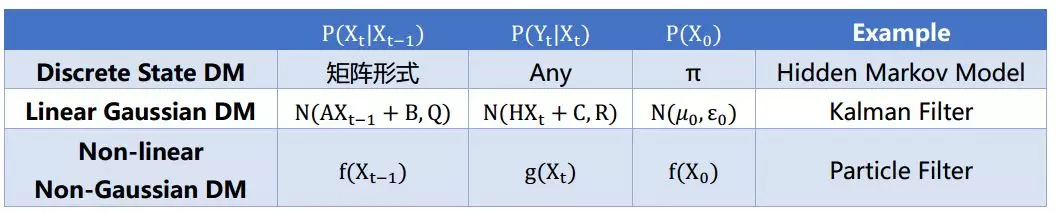
离散状态的动态系统的例子就是隐马尔科夫模型（HMM）。它由一个State Transition Matrix $P(x’\mid x)$，Measurement Matrix $P(y\mid x)$和一个Initial State π组成。注意：HMM 的状态X必须是离散值，而不是连续值，否则 HMM 的状态转移矩阵就是无穷大的。而对Measurement Y没有做要求。
线性高斯动态系统和非线性非高斯动态系统的状态是连续的，线性高斯的State Transition Matrix和Measurement Matrix对应服从高斯分布，而非线性非高斯则可以是任意的。线性高斯动态系统的例子是Kalman Filter，而非线性非高斯的例子是Partical Filter

关于例子

HMM上的常用的操作，一是 uncertainty measurement，已知模型参数和一个观测序列，求它产生的概率，二是 parameter learning，顾名思义就是去对λ = {A, B, π}进行求解。还有一种是做 variable Inference: 在 B 发生的条件下，A 发生的概率 $P(B\mid A)$
卡尔曼滤波是线性动态系统的一种，它的图模型也和 HMM 一样，只是状态取值是连续值，并且它的噪声服从零均值高斯分布，transition probability 和 measurement probability 都服从高斯分布。卡尔曼滤波上的常用操作是 filtering, 给定 T = 1 到 t 时间的观测值，希望对时间 T=t 时的状态进行求解，目标为$P(X_{t}\mid Y_{1}, Y_{2}, … , Y_{t})$。这个filtering是不断的 predict （求解$P(X_{t}\mid Y_{1}, Y_{2}, … , Y_{t-1}) $）和不断 update（求解$P(X_{t}\mid Y_{1}, Y_{2}, … , Y_{t})$）的过程。如下图：
Particle filter 可以看错是一种MC Sampling的算法。具体来说他是建立在Sequential Importance Sampling（SIS）基础之上的。这个SIS算法是为了解决 Importance Sampling 的不能很好处理高维数据的问题，SIS 旨在对每个样本一维一维的进行采样。particle filter 是通过使用了SIS 进行求解的模型，其中 filtering 的分布由采样数据的位置和其权重来刻画
Particle filter 与 Kalman filter 的区别在于，后者认为 measurement 和 transfer probability服从高斯分布，从而 filtering 的分布也服从高斯，他建立起的是 t 时刻和 t+1 时刻 filtering 高斯分布的参数联系；而 particle filter 可以适用于任何分布，所以求解麻烦，转而求助于 SIS 的方法，以当前时刻采样出来的 particle 的位置和权重来表示当前时刻的 filtering 分布。

1. Markov Process

上回，我们说到了动态系统。以HMM模型为例，它由状态，状态转移和观察值三部分组成，用来刻画随时间变化的事物。实际上，我们可以把动态系统看做更为广泛的模型：马尔科夫过程（Markov Process，MP），或者被叫做马氏链（Markov Chain）。

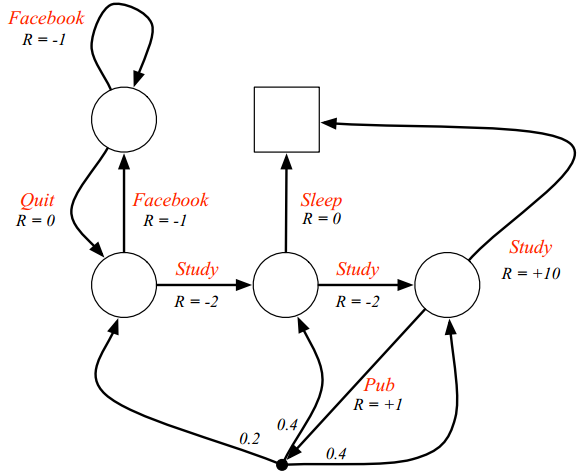
MP是一个状态序列满足马尔科夫条件独立性假设（即给定当前时刻的状态，下一时刻的状态与历史时刻的状态保持独立）的随机过程 $P(S_{t+1}\mid S_t) = P(S_{t+1}\mid S_1, S_2, ..., S_t)$ MP由两个部分组成：有限状态集合$S$和状态转移矩阵$P$，$P_{ss’}=P(S_{t+1}=s’\mid S_{t}=s)$。以下图为例，这是一个学生上课的MP图。学生需要听过三节课之后才能通过（pass）本门课，圆圈和方块表示状态，其中方块表示终止状态（只进不出），边上的数字表示状态转移概率。在第一节课的时候，同学可能会开小差，去刷facebook，并且一旦开始刷facebook，就会有极大的概率（0.9）一直刷下去。同理，也可能上课睡觉，或者课后去酒吧（pub），喝得烂醉之后重新听课。

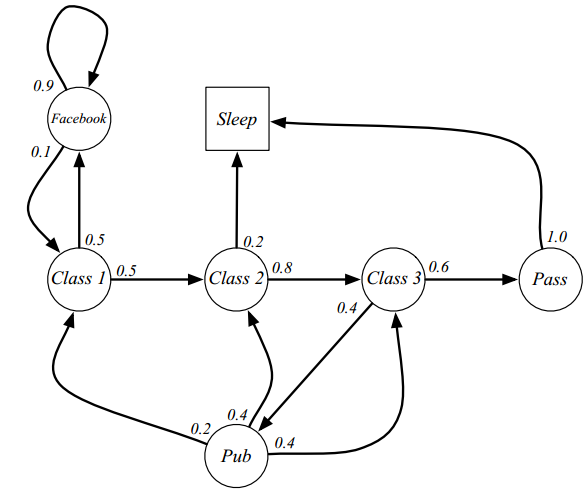
对于HMM模型来说，他还存在观察量（Observations）。准确的来说，HMM其实是一个部分可观察的马氏链（Partially Observable Markov Chain ），因为当前的观察值并不足以完全确定当前所处的状态，就像只有视觉信号的机器人无法全面感知周围的环境一样。如果Observations = State，观察能全面刻画所处的状态信息，那么就叫Full Observability。

无论观察是否全面，MP通过$S$和$P$刻画了状态随时间的转移。如果学生上课的MP图以Class 1作为开始状态，那么，能够得到以下的状态序列

C1 C2 C3 Pass Sleep
C1 FB FB C1 C2 Sleep
C1 C2 C3 Pub C2 C3 Pass Sleep
……..

对于每一个状态序列，总是在终止状态下结束（当然，并不是所有的MP都含有终止状态，这时的状态序列将一直持续下去）。每一个序列都被称作是一个episode。这样的episode其实就是一条时序数据啦。

2. Markov Reward Process

上次说到了Markov Process，他由两部分组成，有限状态集合S和状态转移P。本次我们介绍Markov Reward Process（MRP），他是一个特殊的Markov Process，因为MRP的每个状态上都被附上一个值，这个值被称为Reward。同样，我们以学生上课的状态图为例，这次在每个状态里都附上了Reward（图中红色R）。学生通过考试（pass）可以得到10分的Reward，但是上课的过程是痛苦的，这里给了-2的Reward。

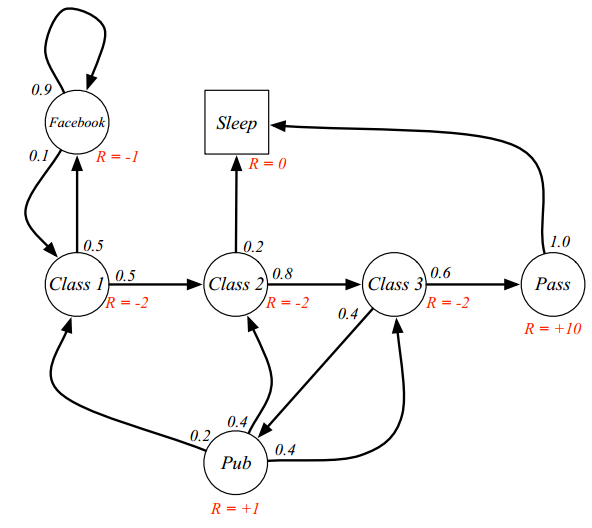
相比MP，MRP由四个部分组成：

有限状态集S
状态转移P，$P_{ss’}=P(S_{t+1}=s’\mid S_{t}=s)$
Reward函数 R，$R_{s}=E[R_{t+1}\mid S_{t}=s]$。注意状态s上的Reward是一个期望值
折扣因子（Discount Factor）$\gamma \in [0, 1]$。

在MRP中，Reward描述了某个状态下的奖励值。在上面的例子中，通过考试（Pass）以最高的奖励（10）来吸引学生向该状态转换。那么折扣因子用来干啥？实际上，MRP并不关心单独某个状态下的Reward，而是喜欢一个Reward的累加量，叫Return。Return G的定义如下： $G_t=R_{t+1}+\gamma R_{t+2} + ... = \sum_{k=0}^\infty \gamma^k R_{t+k+1}$ $G_{t}$ 是在第t时刻的Return。从形式上看，Return计算了从t时刻的某个状态开始，某一个episode所获得的所有discounted Reward的总和。这里的折扣因子是一个0到1之间的数，对于第k+1时刻，累加的reward是$\gamma^k R$，因此时刻越久远，所计算的reward越小。$\gamma$越大，衰减也就越慢。当$\gamma=1$的时候，称为undiscounted MRP。

那为什么需要discount呢？

避免无穷值（万一MRP没有终止状态，或者MRP中有环）。
保留对未来的不确定性。（注意，$R_{s}$是一个期望值，$R_{t}$不是）
其他解释：现在的钱比未来更值钱

因此，我们可以使用Return来表示从一个状态开始的一个episode所带来的奖励。我们以上次的episode为例，计算他们的Return（这里假设$\gamma=1/2$）：

C1 C2 C3 Pass Sleep ：G1=-2 -2* (1/2)-2* (1/4)+10* (1/8)
C1 FB FB C1 C2 Sleep ：G1=-2-1* (1/2) -1 * (1/4) -2* (1/8) -2 *(1/16)

那么，如果我们能得到很多个从同一个状态开始的episodes，便可以用它们来衡量该状态的好坏了（从好的状态开始采样，更容易得到更大的return）。对于状态好坏的衡量，MRP采用了Value Function，准确的说，是叫State Value Function： $v(s)=E[G_t\mid S_t=s]$ 状态价值函数衡量了在某一状态s下，所能获得的Return的期望。它可以看做是对Return的一种预测。那么，对于学生MRP例子，我们可以得到下图（$\gamma=1$），图中红色的数字就表示某状态的state value function的大小。比如对于Pass而言，只有一条路径到终止状态，那么他的v(s)就等于10

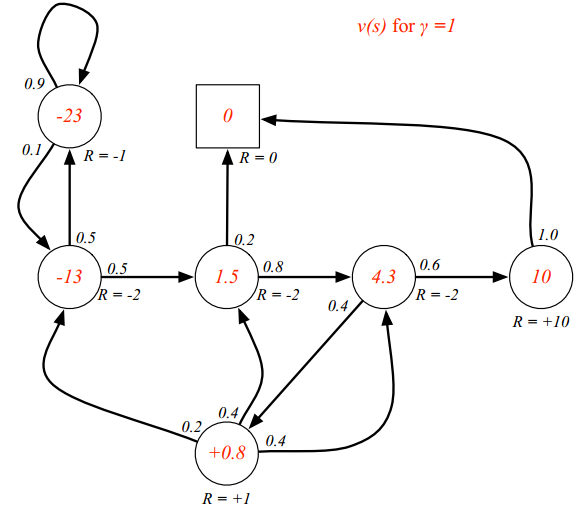
那么，其他状态的v是怎么计算的呢？这就要引入一个公式了，叫Bellman Equation。具体来说，它认为一个状态的v函数可以分解成两部分

immediate reward $R_{t+1}$
下一个状态的discounted $\gamma v(S_{t+1})$

用数学语言就是说：

\[v(s)=E[G_t\mid S_t=s]\\ =E[R_{t+1}+\gamma R_{t+2} + \gamma^2R_{t+3}+...\mid S_t=s]\\ =E[R_{t+1} + \gamma G_{t+1}\mid S_t=s]=E[R_{t+1} + \gamma v(S_{t+1})\mid S_t=s]\]

所以，Bellman Equation的形式如下。注意，在状态s的时候，我们并不知道下一个状态会是啥，所以公式中使用了$S_{t+1}$表示，而不是$s_{t+1}$ $v(s)=E[R_{t+1} + \gamma v(S_{t+1})\mid S_t=s]$ 也就是说，我们需要遍历下状态空间，如下所示，s’表示下一个状态

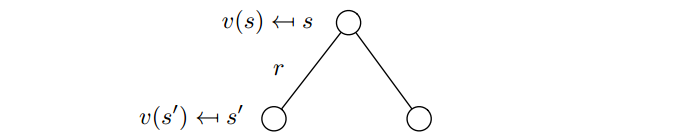
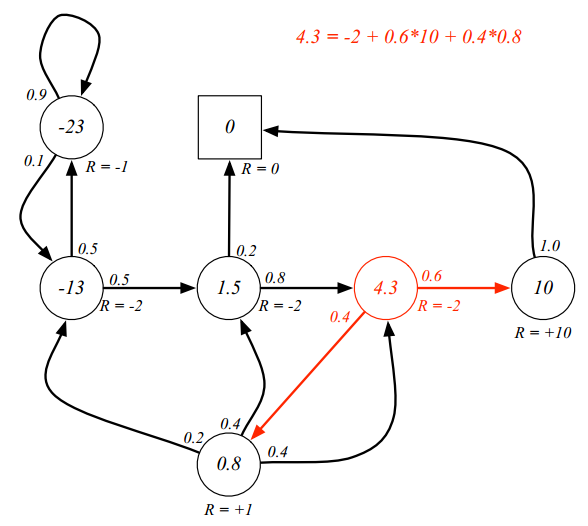
对应的公式变成： $v(s)=R_s + \gamma \sum_{s' \in S}P_{ss'} v(s')$ 我们来看看，学生MRP例子是不是符合这个式子（废话，当然是符合）

对于这个形式来说，可以写成矩阵的形式求解：

\[v=R+\gamma Pv = \begin{bmatrix} v(1) \\ ... \\ v(n) \end{bmatrix} = \begin{bmatrix} R_1 \\ ... \\ R_n \end{bmatrix} + \gamma \begin{bmatrix} P_{11} & ... & P_{1n}\\ ... &... & ...\\ P_{n1} & ... & P_{nn} \end{bmatrix} \begin{bmatrix} v(1) \\ ... \\ v(n) \end{bmatrix}\]

对应的闭式解是：

\[v=(I-\gamma P)^{-1}R\]

当然，计算量很大，求逆是O(n^3)的复杂度，当状态多了，这是很恐怖的。当然也有很多的高级算法啦，比如动态规划，蒙特卡洛和Temporal-Difference learning (TD Learning)等等。之后我们慢慢推送，不急不急。。

3. Markov Decision Process

上回说到了MRP，这次我们做进一步的扩展，它的名字叫做Markov Decision Process (MDP)。它使得系统加入更多交互属性，可以用来刻画序列决策过程。与MRP相比，MDP加入了决策的动作。MDP由以下五个部分组成

有限状态集合S
有限动作（决策）集合A
状态转移P，$P_{ss’}^a=P[S_{t+1}=s’\mid S_{t}=s, A_{t}=a]$
奖励函数R，$R_{s}^a=E[R_{t+1}\mid S_{t}=s,A_{t}=a]$
折扣因子$\lambda \in [0,1]$

MRP中，处于某个状态的事物可以做出一个决策动作。根据所处的状态以及所做的决策动作，该事物会获得一个reward，然后转移到新的状态。下图中就是大家熟悉而又喜爱的学生状态图，图中红色的字表示action。

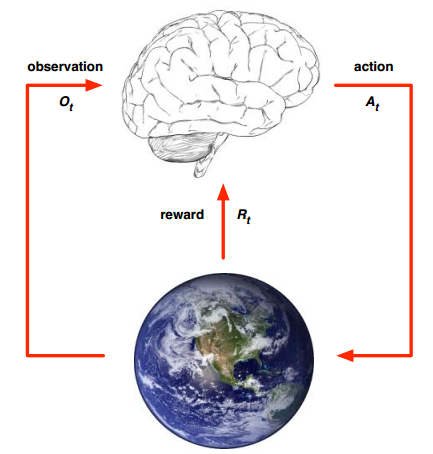
实际上，在MDP中有两个角色：agent和environment。整个MDP就是agent和environment之间不断玩耍交互的过程。agent在第t时刻处于某一个state，agent做出一个action，然后收到一个reward；environment看到agent的action之后，将发送一个reward给agent，然后agent的state被转换。

实际上，agent往往并不能完全察觉自己处于什么样的状态，它只能通过对外界的观察（observation）来推断自己的状态（也就是说，这是partially observable）。所以整个过程就变成了下图所示：agent只接收到对state的观察。

那么，agent为什么需要从observation中推断出state？这是因为MDP是state满足马尔科夫条件，而不是observation。一般来说，可以认为state是history of observations, action和reward的函数，即

\[S_t=f(H_t)\\ \mbox{history：}H_t=O_1, R_1, A_1, ..., A_{t-1}, O_{t}, R_{t}\]

因此，agent的目的就是要通过观察state，做出决策动作，以最大化能获得的累计reward。那么要怎么出招呢？agent需要一个出招秘籍，这个秘籍被称为agent的policy。policy是在给定state下，agent动作的分布 $\pi(a\mid s)=P(A_{t}=a\mid S_t=s)$ 在MRP中，我们引入了State value function来衡量一个state的好坏。在MDP中，加入了动作之后，自然我们想要知道在给定state下，做出每个动作的好坏。这个功能是通过Action value function（或者叫Q函数）来实现的：

\[q_\pi(s,a)=E_\pi[G_t\mid S_t=s,A_t=a]\]

同样，state value function的Bellman Equation同样也适用于Q函数

\[v_\pi(s)=E_\pi[R_{t+1}+\gamma v_\pi(S_{t+1})\mid S_t=s]\\ q_\pi(s,a)=E_\pi[R_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1})\mid S_t=s, A_t=a]\]

事实上，MDP中state s和action a就是这么交替的向后执行：在一个状态下，从动作空间A中选择做出某个动作a，然后不同的a将被转换到不同的新state下。用图片表示则是：

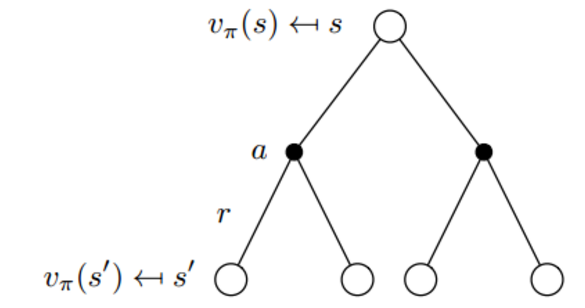
同理，我们也可以从某个action出发，转移到某个状态，在新状态下做出下一个动作：

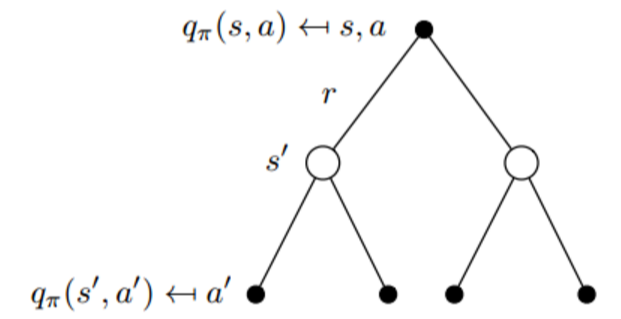
我们可以便可以把Bellman Equation进一步写成：

\[v_\pi(s) = E_\pi[R_{t+1} + \gamma v_{\pi}(S_{t+1}) \mid S_t=s] = \sum_{a\in A} \pi(a\mid s) q_{\pi}(s,a)\\ q_\pi(s,a) = E_\pi[R_{t+1} + \gamma q_{\pi}(S_{t+1}, A_{t+1}) \mid S_t=s, A_t=a] = R_s^a + \gamma \sum_{s' \in S}P^a_{ss'} v_{\pi}(s')\\ v_\pi(s) = \sum_{a\in A} \pi(a\mid s) \left( R_s^a + \gamma \sum_{s' \in S}P^a_{ss'} v_{\pi}(s')\right)\]

以下面的例子来说明，假设跳转概率没有特别说明的话，都是0.5，否则标注在边上。那么就可以验证下图中红色状态的state value function

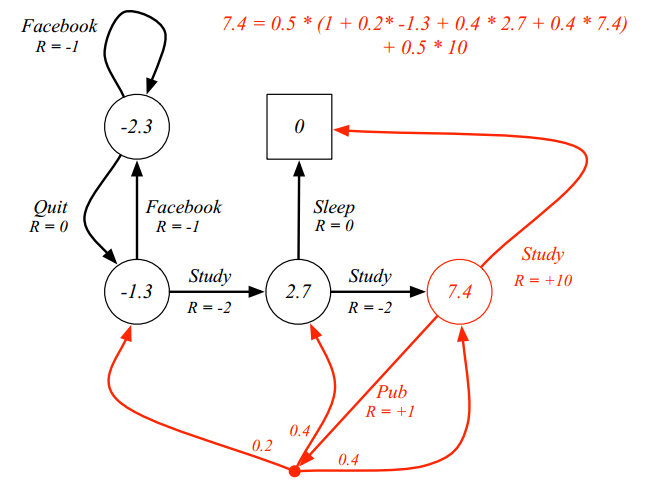
作为agent，他的目的是最大化最后的累计reward。为了达到这个目的，agent需要按照一个最好的policy来出招。实际上，对于任何一个MDP来说，一定存在一个（或者多个）最优policy $\pi^{\star}$ 。而最优的policy对应了最优的state value function $v_\star (s)$和最优的action value function $q_{\star}(s,a)$。他们分别表示在所有可能的policy下，所能达到的最大值，这个最大值就预示着在给定MDP下的做好结果

\[v_*(s)=\max_\pi v_\pi(s)\\ q_*(s,a)=\max_\pi q_\pi(s,a)\]

当我们知道最优的value function的时候，agent的最优策略也就知道了：

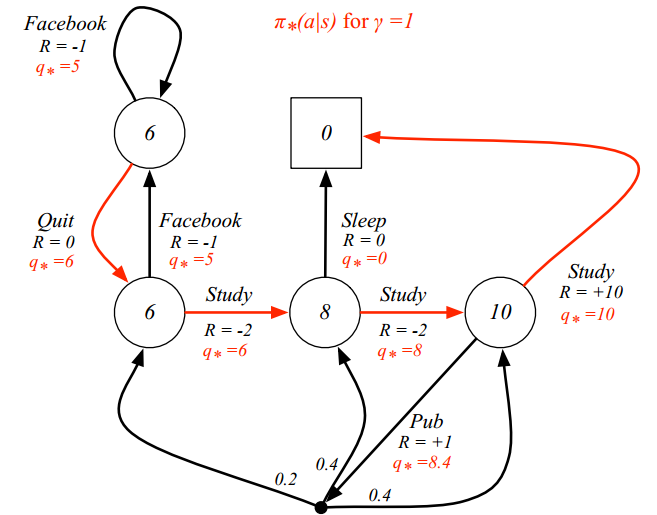
\[\pi^*(a\mid s) = \left\{\begin{matrix} 1 \mbox{ if }a=\arg\max_{a\in A}q_*(s,a) \\ 0 \mbox{ otherwise} \end{matrix}\right.\]

比如下面的例子中的最优策略是红线，可以看出，学习才是最好的出路（手动滑稽）。

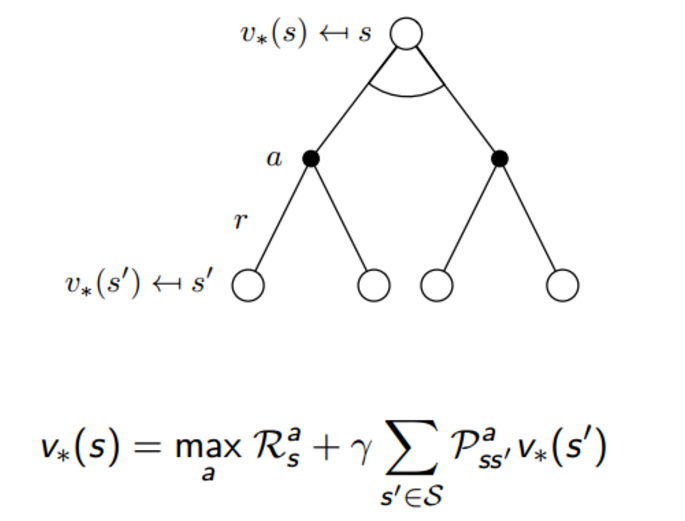
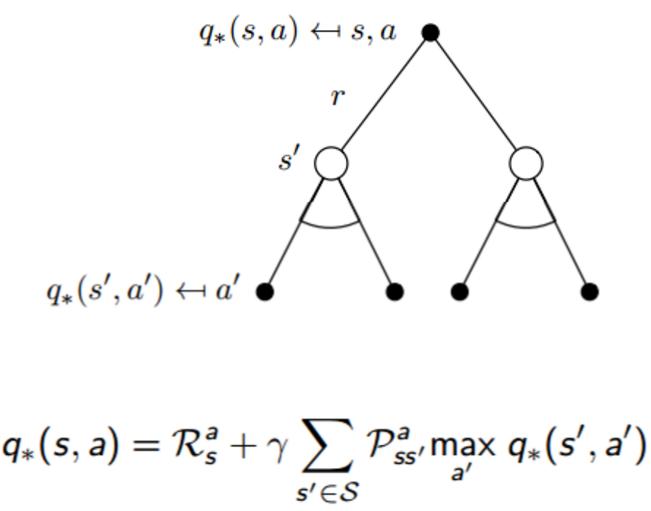
图中的结果是怎么计算出来？这又要用到一个叫Bellman Optimality Equations。总的来说，整个过程还是步步为营的。首先，$v(s)$是在状态s下所能得到return的期望，$q(s,a)$是在给定状态s下，作出动作a之后所能得到的return的大小，然后，在作出动作a之后，将跳转到另一个新状态s’。因此，两者满足

\[v_*(s)=\max_a q_*(s,a)\\ q_*(s,a) = R_s^a + \gamma \sum_{s' \in S} P_{ss'}^a v_*(s')\]

那么，两者结合起来就是

实际上，Bellman Optimality Equation是非线性的，他不能像Bellman Equation一样有闭式解（虽然复杂度很高），但是还是有很多方法可以用来求解。比如Value Iteration, Policy Iteration, Q-learning和Sarsa等等。

4. Reinforcement Learning

从Markov Process，Markov Reward Process到Markov Decision Process，写了这么多，就是引出Reinforcement Learning（RL），几乎所有的RL问题都可以转换成MDP问题。当然了，当前RL研究的问题远不止之前我们所介绍的内容。下面是几个RL的应用例子：

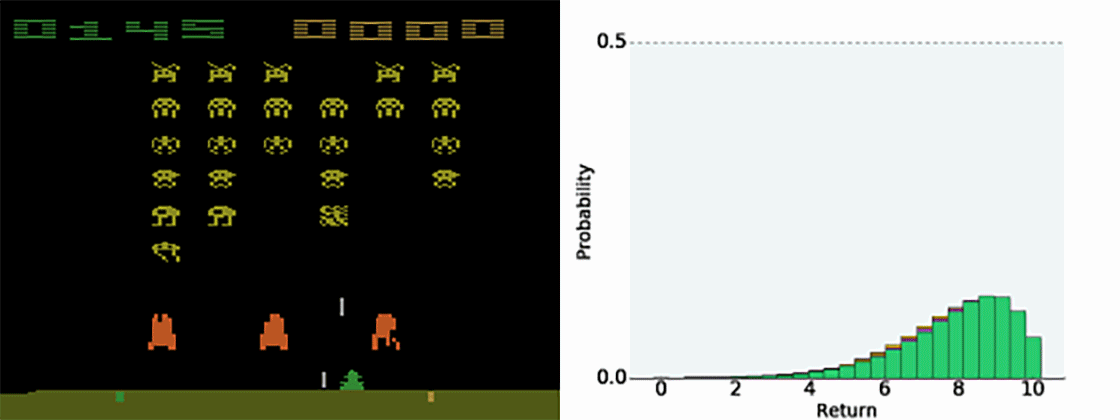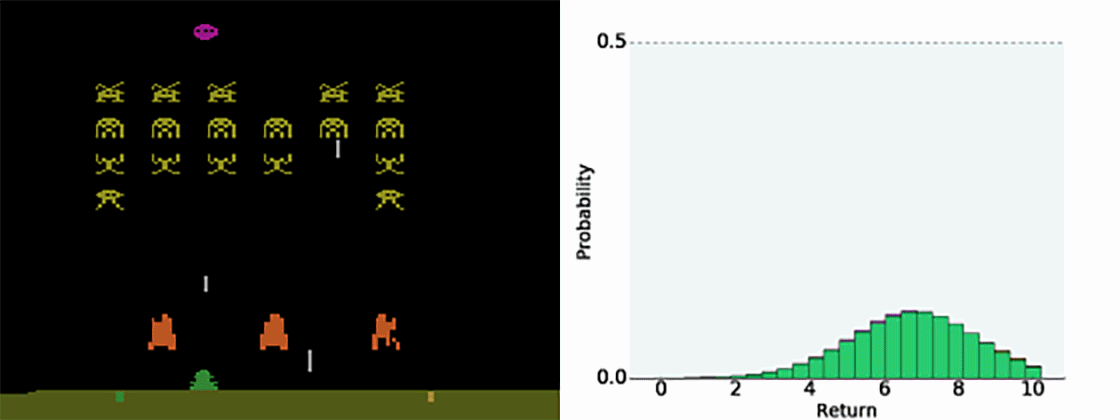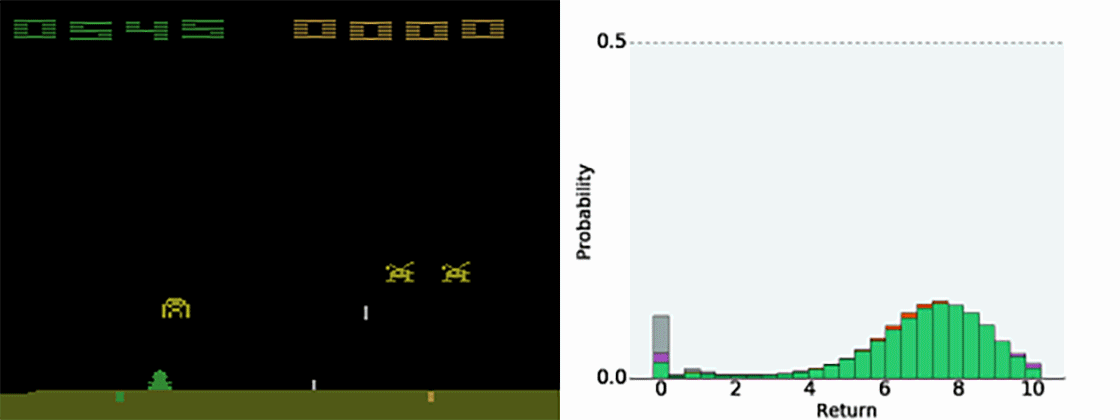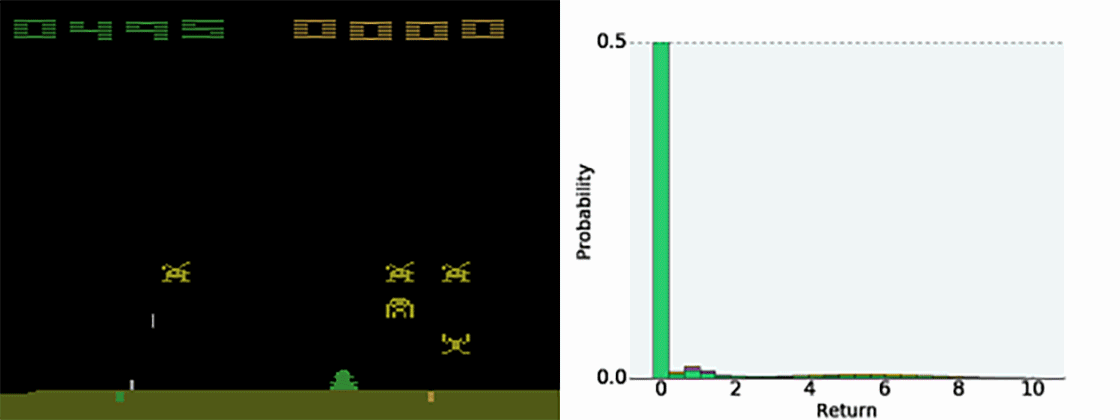
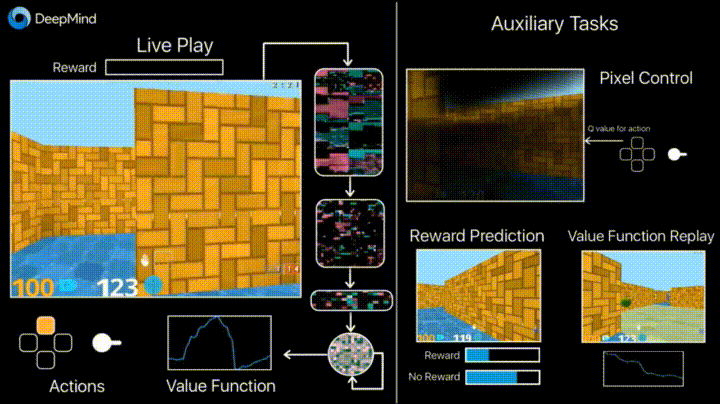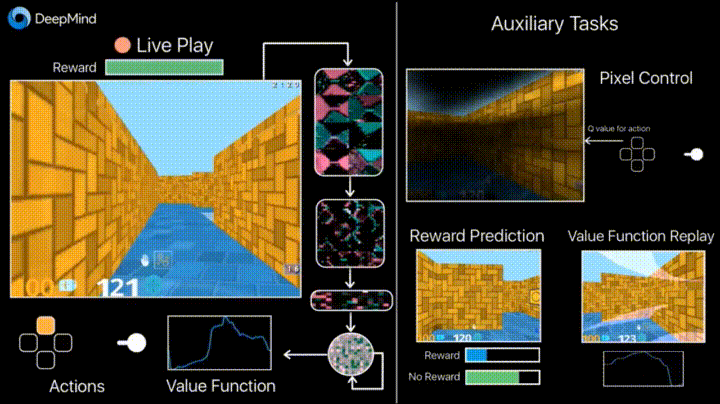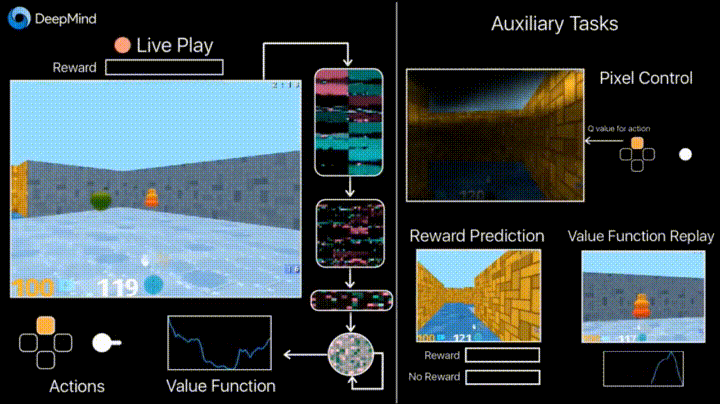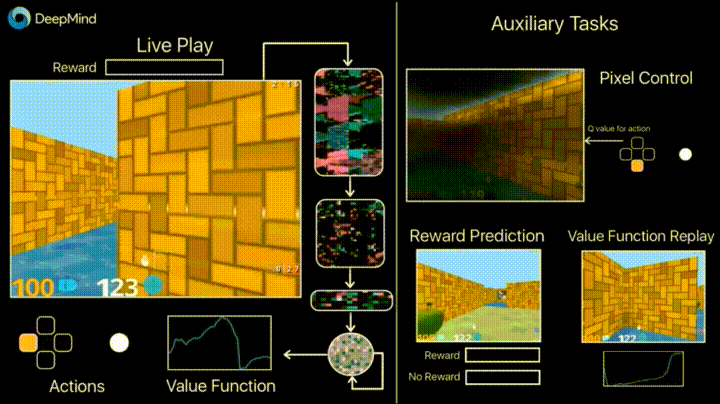
一般来说，机器学习可以分为三类：监督学习，无监督学习和强化学习（怎么可能是半监督学习）。在监督或无监督学习中，我们总是把目标数学化成优化loss的形式（即便，目标任务并不是最小化模型损失），而强化学习是对对序列动作建模，通过reward机制建立与任务之间的联系，它给我们提供了一种能够更为直接地去优化任务本身的方法。也就是说，有时候，人们首先是根据监督或者非监督模型的输出结果，然后针对任务作出决策（比如先判断眼前的动物是猫还是老虎，再决定我们要不要逃跑）。强化学习是一步到位，提供了从what we receiving到what we doing的一个close loop。最后，世间任务千千万，并不是所有的任务都可以明确写出优化目标，对于有些任务监督或者非监督学习，他们是不适用的（就比如下围棋AlphaGo），这也是强化学习另一个优势。PS，这也并不是说监督和非监督学习没啥用，不要偏激的理解，强化学习当然也不是万能的（钱才是）。

只能说明的是，RL虽然有reward反馈，但是，它并不是监督学习：

RL的反馈是可以有时延的。实际情况下，并不是做一个动作之后一定会收到一个真正的reward，比如有的游戏要玩到结束之后，才会收到reward，胜利+1，失败-1。监督学习的标签则不会这样
RL处理的是时序episode，监督学习是iid data
agent的决策动作是会影响下一步的进展的。

和MDP一样，RL的目的在于最大化累计reward。这也是RL的Reward Hypothesis：所有的目标都可以被描述成最大化累计reward，如下式，其中r是reward函数

\[\max_\pi E_\pi \left[ \sum_{t}r(s_t,a_t) \right]\]

一般来说，RL有两类任务：

Prediction：给定policy，估计未来, 找出value function
Control：在所有可能的policy中，最好的value function是啥？哪个是最好的policy？

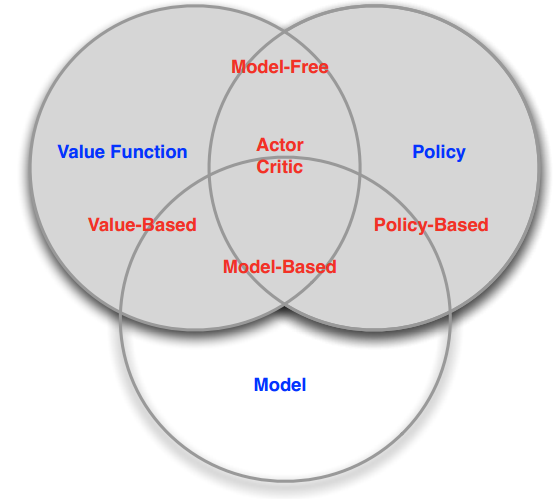
这两类任务可以在不同的背景下完成，这里的背景指的是environment或者model是否已知：agent是否知道状态空间，状态转移以及reward function等等。所以强化学习可以分为

Model-Free RL：不知道model（一般来说是指不知道状态转移以及reward function）
Model-Based RL：知道model

另一方面，强化学习还可以分为

value-based RL：在没有明确的policy下，去找value function
policy-based RL：在没有value function的条件下，去找policy
Actor-critic RL：用当前的policy来估计value ，并用它来提升policy

总的来说，可以用下图表示

RL的过程可以看做是agent和environment之间的游戏，是state和action之间的转换游戏，分别对应了transition和policy。他们可以用下面的图例过程表示。这里的参数$\theta$是用来parameterize策略的（比如使用神经网络来刻画policy，那么$\theta$就是神经网络的参数）。

实际上，这个过程是一个Markov Chain on state and action!

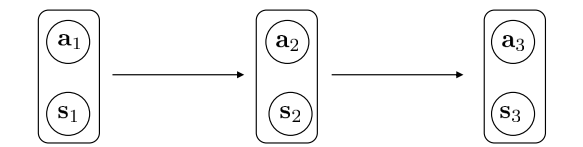
满足

\[p((s_{t+1},a_{t+1})\mid (s_{t},a_t))=p(s_{t+1}\mid s_t,a_t)\pi_\theta(a_{t+1}\mid s_{t+1})\]

那么给定一个episode，他的概率可以写成

\[p_\theta(s_1,a_1,...s_T,a_T)=p(s_1) \prod_{t=1}^T \pi_\theta(a_t\mid s_t)p(s_{t+1}\mid s_t,a_t)\]

5. Policy Gredients

对于RL来说，我们想要找出一个最好的policy来完成任务，比如打游戏的时候见到坑要知道跳，见到怪要知道打，见到金币得知道吃等等。前面说的RL的最终任务就是要最大化期望累计reward，这里的最大化是通过找一个最优的policy来实现的。下面公式中的$\theta$是policy $\pi$的参数（比如我们用神经网络来计算policy，那么$\theta$就是网络的参数）

\[\theta^*=\arg\max_\theta E_{\tau \sim \pi_\theta(\tau)} \left[ \sum_{t=1} \gamma^{t-1} r(s_t,a_t) \right]=\arg\max_\theta \int \pi_\theta(\tau) r(\tau) d\tau\\ \pi_\theta(\tau)=p_\theta(s_1,a_1,...,s_T,a_T)=p(s_1) \prod_{t=1}^T \pi_\theta(a_t\mid s_t)p(s_{t+1}\mid s_t,a_t)\\ r(\tau)=\sum_{t=1} \gamma^{t-1}r(s_t,a_t)\]

学过监督学习的我们知道，在监督学习中很多很多的算法都是可以通过梯度下降的方法来求解的，那么给定RL的目标方程，我们同样也可以使用梯度的方法来更新求解policy，使得最大化期望累计reward。也就是说，只需要用积分那一项（令他为$J(\theta)$）对$\theta$求导就可以了。注意，这里我们假定了policy是可导的。policy的形式往往是人定的（比如gaussian，神经网络等等），所以policy可不可导也是可控的。

\[\bigtriangledown_\theta J(\theta)=\int \bigtriangledown_\theta\pi_\theta(\tau) r(\tau) d\tau\]

问题就变成求出$\bigtriangledown_\theta\pi_\theta(\tau)$就ok了，大牛们当然不会直接去求解这一项，因为从最开始的式子里可以看到，$\pi_\theta(\tau)$涉及到多项相乘，直接求导会很心累。所以大牛提出了一个 convenient identity

\[\bigtriangledown_\theta\pi_\theta(\tau)=\pi_\theta(\tau) \frac{\bigtriangledown_\theta\pi_\theta(\tau)}{\pi_\theta(\tau)}=\pi_\theta(\tau)\bigtriangledown_\theta log \pi_\theta(\tau)\]

其中在贝叶斯里往往把$\bigtriangledown_\theta log \pi_\theta(\tau)$叫做score function。比如以一次动作为例，当我们用softmax来近似policy $\pi_{\theta}(\tau)$的时候（这叫做Softmax Policy），这时的score function可以写成下式，这个式子衡量了当前动作相比于平均动作的好坏。

\[\pi_\theta(a\mid s)= \frac{e^{\phi(s) ^T \theta }}{\sum_a e^{\phi(s) ^T \theta}} \\ \bigtriangledown_\theta log \pi_\theta(a\mid s)=\phi(s) - \sum_{a' \in A} \pi_\theta(a'\mid s) \phi(s)\]

同理，如果我们使用的是Gaussian，也就对应着叫Gaussian Policy:

\[\pi_\theta(a\mid s)=N(\phi(s) ^T \theta;\Sigma)\\ log\pi_\theta(a\mid s)=-\frac{1}{2} \mid \mid \phi(s) ^T \theta-a\mid \mid _\Sigma^2 +const\\ \bigtriangledown_\theta log \pi_\theta(a\mid s)=-\frac{1}{2}\Sigma^{-1}(\phi(s) ^T \theta-a) \phi(s)\]

这个score function的含义还是类似的，他也刻画了action与平均action的差异。注意，以上两个例子中，我们都假定了policy中的输入参数state是policy 参数$\theta$和state feature $\phi(s)$之间的linear combination $\phi(s) ^T \theta$。如果需要加大表达能力，则完全可以采用其他函数，比如神经网络$f(s)$。

现在，我们把convenient identity带入到$\bigtriangledown_\theta J(\theta)$中就得到

\[\bigtriangledown_\theta J(\theta)=\int \pi_\theta(\tau)\bigtriangledown_\theta log \pi_\theta(\tau) r(\tau) d\tau=E_{\tau \sim \pi_\theta(\tau)} [\bigtriangledown_\theta log \pi_\theta(\tau) r(\tau)]\\ =E_{\tau \sim \pi_\theta(\tau)} \left[ \left(\sum_{t=1}^T \bigtriangledown_\theta log \pi_\theta(a_t\mid s_t) \right) \left( \sum_{t=1}^T \gamma^{t-1} r(s_t,a_t)\right) \right]\]

也就是说，这个identity可以在保证期望形式不变的条件下，简化计算。形式优美，让当下RL科研工作者沿用至今，是一个常用的方法。那么这个导数里的期望怎么算？采样！

到这里，policy gradient和极大似然估计还是比较神似的。只是说，RL中对episode加权咯，优化的结果就是，它会偏好reward高的episodes，使得它们出现概率更高，相反不好的action所导致的episode，出现概率低。

\[\bigtriangledown_\theta J(\theta) \approx \frac{1}{N} \sum^N_{i=1} \left( \left(\sum_{t=1}^T \bigtriangledown_\theta log \pi_\theta(a_{i,t}\mid s_{i,t}) \right) \left( \sum_{t=1}^T \gamma^{t-1} r(s_{i,t},a_{i,t})\right) \right)\\ =\frac{1}{N} \sum^N_{i=1} \bigtriangledown_\theta log \pi_\theta(\tau_i) r(\tau_i)\\ \bigtriangledown_\theta J_{ML}(\theta) \approx \frac{1}{N} \sum^N_{i=1} \left(\sum_{t=1}^T \bigtriangledown_\theta log \pi_\theta(a_{i,t}\mid s_{i,t}) \right)=\frac{1}{N} \sum^N_{i=1} \bigtriangledown_\theta log \pi_\theta(\tau_i)\]

其实，REINRORCE算法就是这么做的，这里折扣因子$\gamma=1$

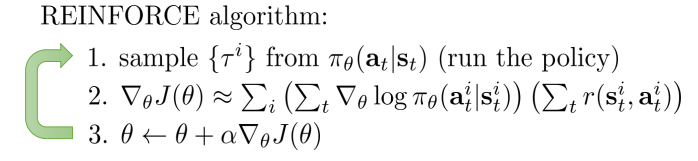
该算法会在每次迭代中，从当前的policy中采样，也就是用这个policy来玩一下游戏，得到一些episodes，然后用采样样本计算梯度，执行梯度上升算法（因为我们要max，而不是min）以提升当前policy。所以REINFORCE算法是一种On-Policy Monte-Carlo Policy-Based RL算法。这里的On-policy指用于学习policy $\pi$的样本是原于$\pi$本身的；相反则是off-policy，用于学习policy $\pi$的样本是原于其他策略。

5.1 Improved Policy Gradients

Policy Gradient和大家常用的SGD同样都有high variance，slow convergence以及难以选择learning rate的问题。对于variance的问题，可以想象成如果policy空间铺得太开，就不容易选中最应该选择的action（比如高斯的均值处）。下面就reduce variance做一个总结，其他的问题可以通过叫natural policy gradient的方法解决。

一般来说，降低variance，可以走两种方案

Causality, reward to go：今天做的动作，不会影响昨天发生的事
Baselines：选一个比平均动作更好的动作

Causality, Reward to go

简单的形式如下。唯一不同的地方就是对reward的sum，不在是从1开始，而是从当前action发生的时刻开始，对于当前action动作以前的时刻所产生的reward不在考虑。这时候的方差减小的原因是。。reward叠加的数值变小咯，相对variance也会减少。

Baselines

Baseline想做的是，与其直接最大化每个episode的累计reward，不如最大化每个episode reward 与平均reward的差值，使得episode能做得比平均值更好。对于比平均做得差的，那就降低他的出现概率。

\[\bigtriangledown_\theta J(\theta) \approx \frac{1}{N} \sum^N_{i=1} \bigtriangledown_\theta log \pi_\theta(\tau_i)[ r(\tau_i) - b]\\ b=f(r(\tau))\]

与之前的公式相比，新添加的b并不会带来影响，因为期望是等于0的

\[E[ \bigtriangledown_\theta log \pi_\theta(\tau) b]=\int \pi_\theta(\tau) \bigtriangledown_\theta log\pi_\theta(\tau) b d\tau=\int \bigtriangledown_\theta \pi_\theta(\tau) bd\tau=b\bigtriangledown_\theta \int \pi_\theta(\tau) d\tau=0\]

那么b应该取什么值呢？一开始引入Baseline的原因是为了降低variance，那么引入b之后的variance等于啥呢

\[Var=E_{\tau \sim \pi_\theta(\tau)}[\left( \bigtriangledown_\theta log \pi_\theta(\tau)[ r(\tau) - b] \right)^2] - E_{\tau \sim \pi_\theta(\tau)}[\bigtriangledown_\theta log \pi_\theta(\tau)[ r(\tau) - b] ]^2\]

为了最小化上面的式子，可以对b求导，可以得到下面的第一个式子，但是在实际使用中往往使用第二个，也就是第一个的不加权求和的版本。

\[b=\frac{E\left[(\bigtriangledown_\theta log \pi_\theta(\tau))^2 r(\tau)\right]}{E\left[(\bigtriangledown_\theta log \pi_\theta(\tau))^2\right]}\\ b=\frac{1}{N}\sum_{i=1}^N r(\tau_i)\]

5.2 Off-policy policy gradients

之前说到的policy gradient是on-policy的，我们使用源于同一个policy下的样本来更新policy本身。当然，我们也可以使用off-policy的方式。on-policy的方式，一旦policy改变了，就必须在下一次迭代的时候。重新采样新的episode，折痕inefficient！off-policy是从别的策略（叫做behaviour policy）中采样，来更新我们想要的策略（target policy），这种方式最大的好处就在于可以做policy exploration，而不是仅仅的policy exploitation。啥意思？RL最大的bug就在于policy和value funciton的搜索空间实在是太大了，在寻找最优解的时候，我们要竟可能的去探索未知（exploration），同时需要在已经探索过的地方，充分挖掘，找出最好（exploitation）。这两者之间的矛盾就好比晚饭吃去过的最好餐馆还是去尝试新馆子，新馆子当然会有好有坏。总的来说，off-policy提供了一个behavior policy，以便我们用别的知识来接入。

从别的地方采样，用于自己的任务，这种方式就是大家熟悉而喜爱的Importance Sampling干的事。简单的说，重要性采样提供了直接近似期望的框架，它假定直接从目标分布P(X)中采样无法完成，但是对于任意给定的X值，我们可以很容易地计算P(X)的值。如此，为了计算其期望$E[f(X)]=\int f(X)P(X)dX$，我们希望对P(X)值大（质量大）的区域中尽可能多的进行采样，因为这部分的样本对期望的计算发挥的作用更大。重要性采样，把容易被采样的新的分布Q(X)作为目标采样分布，并且赋予这些采样的样本一定的权重，整个样本上的不同大小的权重值的则构成了真实的P(X)的采样数据，如下所示。

\[E_{x \sim p(x)}[f(x)]=\int p(x)f(x)dx=\int q(x)\frac{p(x)}{q(x)}f(x)dx=E_{x \sim q(x)}[\frac{p(x)}{q(x)}f(x)]\]

那么应用到RL的目标中就是

\[J(\theta) = E_{\tau \sim \pi'(\tau)} [\frac{\pi_\theta(\tau)}{\pi'(\tau)}r(\tau)]\\ \frac{\pi_\theta(\tau)}{\pi'(\tau)}=\frac{p(s_1) \prod_{t=1}^T \pi_\theta(a_t\mid s_t)p(s_{t+1}\mid s_t,a_t)}{p(s_1) \prod_{t=1}^T \pi'(a_t\mid s_t)p(s_{t+1}\mid s_t,a_t)} = \prod_{t=1}^T \frac{\pi_\theta(a_t\mid s_t)}{\pi'(a_t\mid s_t)}\]

对应的梯度是下式，其中第三个式子，是在第二个式子的基础上考虑到Causality之后得到的：第三项表示现在的动作不会影响以前的reward，第二项是表示当前的动作仅仅与之前的策略有关。

\[\bigtriangledown_\theta J(\theta) = E_{\tau \sim \pi'(\tau)} [\frac{\pi_\theta(\tau)}{\pi'(\tau)} \bigtriangledown_\theta log \pi_\theta(\tau) r(\tau)]\\ =E_{\tau \sim \pi'(\tau)} \left[ \left(\prod_{t=1}^T \frac{\pi_\theta(a_t\mid s_t)}{\pi'(a_t\mid s_t)}\right)\left(\sum_{t=1}^T \bigtriangledown_\theta log \pi_\theta(a_{i,t}\mid s_{i,t}) \right) \left( \sum_{t‘=1}^T \gamma^{t'-1} r(s_{i,t'},a_{i,t'})\right)\right] \\ =E_{\tau \sim \pi'(\tau)} \left[ \sum_{t=1}^T \bigtriangledown_\theta log \pi_\theta(a_{i,t}\mid s_{i,t}) \left(\prod_{t'=1}^t \frac{\pi_\theta(a_t'\mid s_t')}{\pi'(a_t'\mid s_t')}\right) \left( \sum_{t‘=t}^T \gamma^{t'-t} r(s_{i,t'},a_{i,t'})\right)\right]\]

5.3 Other Policy Gradients Methods

前面都是要求policy是可导的，但是如果policy实在不可导怎么办？有一个简单的办法就是去一维一维的近似梯度。这个方式很低效而且也会有很大error，但是也算是一种策略嘛

\[\frac{\partial J(\theta)}{\partial \theta_k} \approx \frac{J(\theta+\epsilon u_k)-J(\theta)}{\epsilon}\]

对于REINFORCE算法，他的梯度计算方式下式。这里的$r(\tau)$是整个episode的累计reward，这也就意味着，必须要等到episode执行完了之后才能更新

\[\bigtriangledown_\theta J(\theta)=E_{\tau \sim \pi_\theta(\tau)} [\bigtriangledown_\theta log \pi_\theta(\tau) r(\tau)]\]

这之外还有很多其他的算法针对$r(\tau)$这项做变化

\[\bigtriangledown_\theta J(\theta)=E_{\tau \sim \pi_\theta(\tau)} [\bigtriangledown_\theta log \pi_\theta(\tau) r(\tau)] \rightarrow \mbox{ REINFORCE algorithm} \\ \bigtriangledown_\theta J(\theta)=E_{\tau \sim \pi_\theta(\tau)} [\bigtriangledown_\theta log \pi_\theta(\tau) Q_w(\tau)] \rightarrow\mbox{ Q Actor-Critic algorithm}\\ \bigtriangledown_\theta J(\theta)=E_{\tau \sim \pi_\theta(\tau)} [\bigtriangledown_\theta log \pi_\theta(\tau) A_w(\tau)]\rightarrow\mbox{ Advantage Actor-Critic algorithm}\\ \bigtriangledown_\theta J(\theta)=E_{\tau \sim \pi_\theta(\tau)} [\bigtriangledown_\theta log \pi_\theta(\tau) \delta ]\rightarrow\mbox{ TD Actor-Critic algorithm}\\ \bigtriangledown_\theta J(\theta)=E_{\tau \sim \pi_\theta(\tau)} [\bigtriangledown_\theta log \pi_\theta(\tau) \delta e]\rightarrow\mbox{ TD(lambda) Actor-Critic algorithm}\\ ...\]

6. Actor-Critic Algorithms

6.1 Reduce variance by actor-critic algorithm

之前REINFORCE算法通过$\bigtriangledown_\theta J(\theta) \approx \frac{1}{N} \sum^N_{i=1} \bigtriangledown_\theta log \pi_\theta(\tau_{i}) r(\tau_{i}) $来计算梯度，但是$r(\tau_{i})$只是依赖一个样本episode，这也会带来hige variance（这和SGD一样，mini-batch的variance总比SGD小）。实际上从某个状态出发，可能会有很多中的走法（如下图所示）。一个比较好的替换策略是采用真实的期望reward to go来代替。

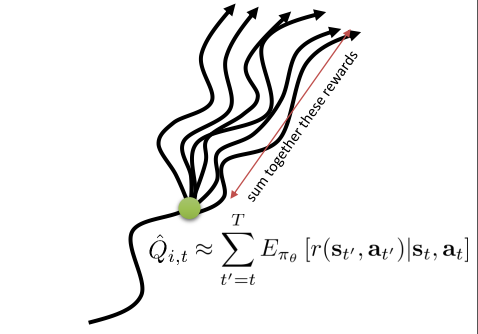
也就是说，我们可以用下式计算梯度以进一步降低方差

\[\bigtriangledown_\theta J(\theta) \approx \frac{1}{N} \sum^N_{i=1} \sum_{t=1}^T \bigtriangledown_\theta log \pi_\theta(a_{i,t}\mid s_{i,t}) Q(s_{i,t},a_{i,t})\]

还可以进一步加入Baseline。之前的b采用的平均return。现在则是采用$V(s_{i,t})$。他也是一种对Q在不同action下的平均。

\[V(s_{t})=E_{a_t \sim \pi_\theta(a_t \mid s_t)}[Q(s_{t},a_{t})]\]

这时候称$A(s_{t},a_{t})=Q(s_{t},a_{t})-V(s_{t})$为advance function，它衡量的同样也是一个action比”平均action”好多少。相比于之前的$r(\tau_{i})-b$，advance function的方差要小很多。那么问题来了，这个advance function要怎么求？我们不知道Q，也不知道V，更不知道A了。

事实上，对于A的求解，在实际算法里只求解V就好了：

\[Q(s_t,a_t)=r(s_t,a_t)+V(S_{t+1})=r(s_t,a_t)+E_{s_{t+1} \sim P(s_{t+1}\mid s_{t}, a_t)}[V(s_{t+1})]\]

如果model是已知的（也就说$P(s_{t+1} \mid s_{t}, a_{t})$），那么上面的式子就可以直接带入A中。如果model是未知的，那么往往采用近似的方法（事实上，就算model已知，也可以采用近似，毕竟计算量小）。这里有两种近似$Q(s_{t},a_{t})$的方式，一种是采用MC采样，另一种是通过bootstrap。

对于MC来说，他会用样本的平均return来代替Q

\[Q(s_t,a_t) = \sum_{t'=t} \gamma^{t'-t} r(s_{t'},a_{t'})\\ A_{MC}(s_t,a_t) \approx \sum_{t'=t} \gamma^{t'-t} r(s_{t'},a_{t'}) - V(s_t)\]

对于bootstrap来说，我们直接用下一个状态来带入就行了，不必去遍历整个状态空间。虽然这个方式损失了一些信息，但是相比于$r(\tau)$的方式，还是要好太多了。

\[Q(s_t,a_t) \approx r(s_t,a_t)+V(s_{t+1})\\ A_{Bootstrap}(s_t,a_t) \approx r(s_t,a_t)+V(s_{t+1}) - V(s_t)\]

那么，我们只用得到V就可以求出A咯。要得到V，就可以用到Actor-Critic Algorithm了。之前在policy gradient中，我们介绍的算法都只是在求policy（也就是actor），而这个算法还要求value（也就是critic干的事）。

Critic：用于更新Value function，判断当前policy的好坏
Actor：接收critic的信息，用于更新policy（update policy in direction suggested by critic）

6.2 Improve policy gradient by critic

那么，怎么用critic，在给定policy的时候求解V呢？这就要用到policy evaluation了。

6.2.1 Policy evaluation with known MDPs

policy evaluation是建立上Bellman Equation之上的。用上一时刻的value function来做更新

\[v_{k+1}(s)=\sum_{a \in A} \pi(a\mid s) \left(R_s^a + \gamma \sum_{s' \in S}P^a_{ss'} v_k(s') \right)\]

简单的说，这是一个迭代的过程，直至收敛：$v_{1} \rightarrow v_{2} … \rightarrow v_{\pi}$。在第k+1次迭代的时候，对于所有的状态s，都需要用第k次迭代得到的v来更新。这个过程是可以保证收敛到真实值上去的。下面是一个经典的例子：给定一个4*4的格子，格子上有两个门（如图中阴影部分），小明需要尽快的从一个门到另一个门，每走一步，小明就会收到-1的reward。当给定一个随机策略（也就说在空白格子上可以等概率的选择任意方向前进），现在要评估每一个格子上的expected return。

在刚开始，初始化v都等于0，然后下一步，我们按照上面的公式进行迭代，可以得出v都变成了-1（两个门的地方，我们不做更新），以此类推

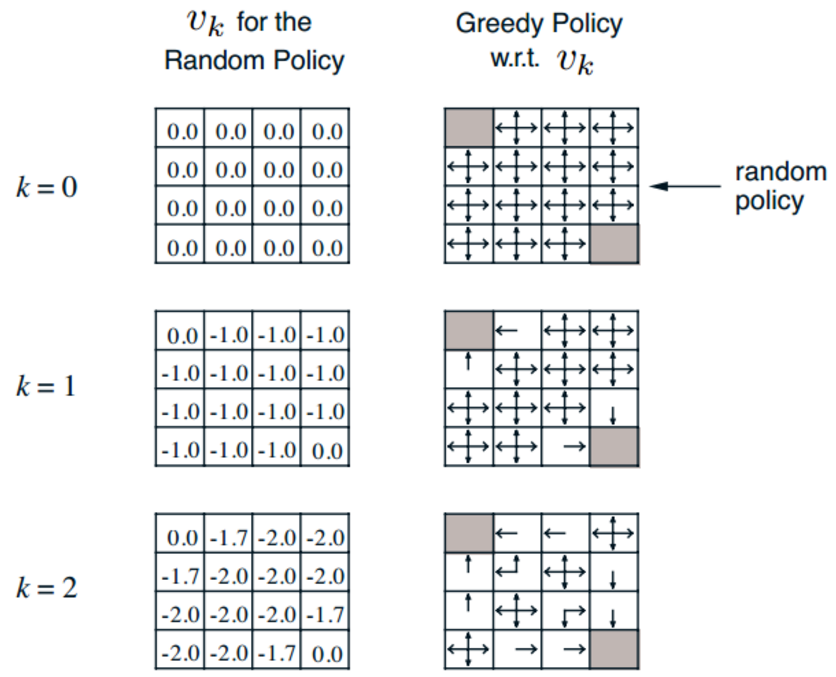
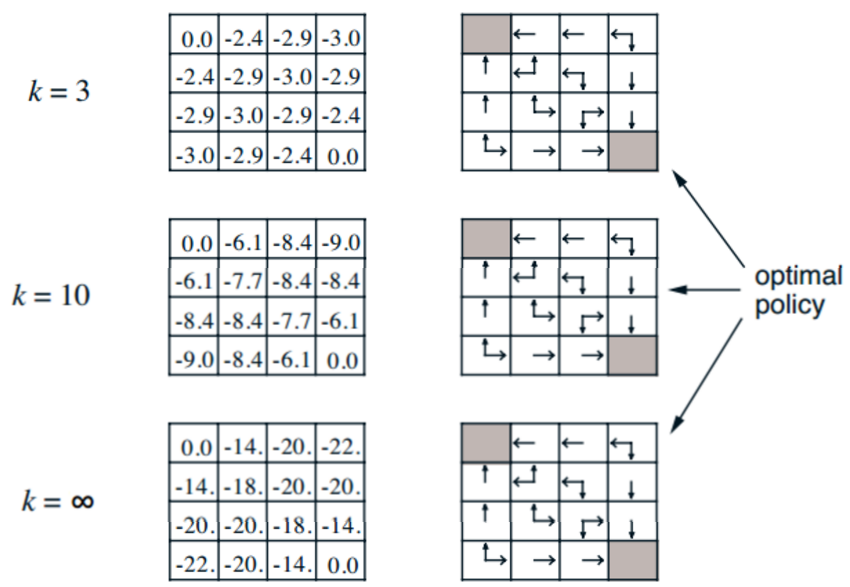
当进行很多次之后，v矩阵就收敛不变了，这时候就得到在随机策略下，各个state的v函数了。左图表示一个迭代之后的结果，也就是迭代之后的state value function。并且每一次迭代之后产生的v都能对应得到一个明确的policy（右图）。注意，右图只是单纯画出来的而已，在evaluation的过程中，并没有更新policy本身。

6.2.2 Policy evaluation with unknown MDPs

前面提到的方式是建立在Bellman方程上的，也就说必须要知道状态转移P。在实际情况下，大多都是不知道的。那么，在不知道MDPs的情况下，如何做Policy Evaluation呢？

6.2.2.1 Monte-Carlo Learning

MC走的就是采样的路，用样本来近似求解，比如用样本均值来近似期望等等。所以，MC的方式是用过样本的平均return来近似State-value function的。但是，MC方法需要对整个episode进行采样，必须要得到整条episode之后，才能做后续的操作（这里隐藏暗示了每一个episode都会terminate），所以MC方法一般是off-line update的。

MC方法一般有两种

First-visit Monte-Carlo Policy Evaluation
Every-visit Monte-Carlo Policy Evaluation

两者之间的差别不大，先说说第一种。假设要对state s计算他的v函数，那么：

采用好多个episodes
遍历每一个episode
1. 如果s在该episode中的第t时刻被第一次访问到了
  1. $N(s) += 1$
  2. $S(s) += G_{t}$
计算$V(s)=\frac{S(s)}{N(s)}$

第二种方式的不同之处在于如果s在该episode中的任何时刻被访问到了，则都进行N和S的更新。另外，更常用的是增量式更新的策略：

\[u_k=\frac{1}{k} \sum_{j=1}^k x_j=\frac{1}{k} \left( x_k + \sum_{j=1}^{k-1}x_j \right) = \frac{1}{k} (x_k + (k-1)u_{k-1})=u_{k-1}+\frac{1}{k}(x_k-u_{k-1})\]

那么，就可以有两种以下更新方式，第一种是常规的MC

\[N(S_t) += 1 \\ V(S_t) \leftarrow V(S_t) + \frac{1}{N(S_{t})} (G_t -V(S_t))\]

第二种是更广泛意义，它用于非稳定环境下的更新问题，对应时间久远的episode就不那么关注了，

\[N(S_t) += 1 \\ V(S_t) \leftarrow V(S_t) +\alpha (G_t -V(S_t))\]

6.2.2.2 Temporal-Difference Learning (TD Learning)

TD Learning不必从完整的episode中学习，反而是采用bootstrapping（引导）的方式进行online的更新。具体来说，TD采用以下的更新方式。其中R是immediate reward

\[V(S_t) \leftarrow V(S_t) +\alpha (R_{t+1} + \gamma V(S_{t+1}) -V(S_t))\]

很明显，TD与MC的第一个不同之处便是：TD采用$R_{t+1} + \gamma V(S_{t+1})$代替了$G_{t}$。这个$R_{t+1} + \gamma V(S_{t+1})$被称为TD target，而$R_{t+1} + \gamma V(S_{t+1}) -V(S_{t})$被称为TD error。这个算法被称为TD(0)算法。TD learning旨在步步为营的优化求解，用下一步的状态来更新当前步，也就不用一次性走完全部的episode。下面是一个例子：预计到家还有多少分钟。从开车到回家的路上，算是一个episode，到家了就terminate。左图是用MC的方式，在episode中的每一步与最后的return的差值$G_{t} -V(S_{t})$用箭头表示，而右图是TD的方法，他的差异是由下一个状态的值决定，而不是最后的$G_{t}$。

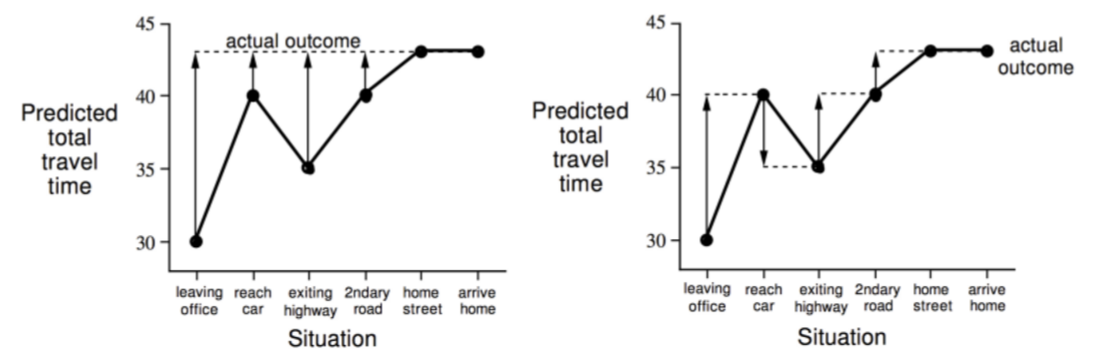
在当前state下，怎么得到下一个state呢？其实，我们直接在当前state下，按照policy走一步，就可以得到下一步的state了。TD(0)算法的伪代码如下：

总的来说，TD和MC的第一个不同之处就是：

MC采用了整个episode的return来做更新，TD采用TD target，可以在线更新
MC方式不能用于没有终止状态的MDP，TD可以
MC采用$G_{t}$来更新，而$G_{t}$是$v_\pi(S_{t})$的无偏估计。原本来说，TD target也是无偏的，但是！实际操作中（如算法中，我们是采用下一步的v的估计量来更新的，这时候的下一步v是不准确的！）是有偏估计的。但是TD方法仅仅依赖一个action，一次transition和一个reward，MC是好多好多个。所以TD的方差远小于MC的
总的来说，MC收敛性好，初值不敏感。TD反之，但是TD效率高于MC
TD target是建立在Markov假设上的，所以要是环境不太满足假设，还是MC的效果会好一些

6.2.2.3 N-step TD & TD($\lambda$)

一个直观的想法是，TD(0)是向前多走了一步，那么能不能多走n步呢？答案当然是可以的，那就是n-step TD算法。

\[G_t^n = R_{t+1} + \gamma R_{t+2} + ... \gamma ^{n-1} R_{t+n} + \gamma^n V(S_{t+n}) \\ V(S_t) \leftarrow V(S_t) +\alpha (G_t^n -V(S_t))\]

正因为n-step TD算法多走的那几步，进一步的降低了TD(0)算法的bias，但是，走多了，方差就会变得大起来。所以n-step TD约等于是一个bias和variance之间的trade-off：多走几步，降低bias，然后截断，之后的步子用V来代替，防止方差变大。当n-step TD之间走到最后，那就变回MC算法

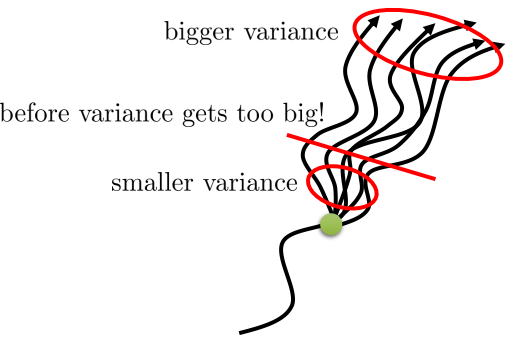
但是要走几步才好呢？答案是不知道。但是一个解决方式是考虑Multi-kernel learning：既然不知道那个kernel好，那就把他们都加起来，取个平均。TD learning也是这个思路。比如对2-step和4-step取均值

\[\frac{1}{2} G^2 + \frac{1}{2} G^4\]

但是，对于不同的n，n-step TD的价值是不一样的。当n比较小的时候，它引入的方差是更小的。所以，在结合多种走法的时候，他们的权重是递降的。并且，如果前n步都打算结合起来，那么就很费时间了，因为每一个n都得求一次，加起来。为了高效的处理这个问题，引入了TD($\lambda$)算法。

首先，TD($\lambda$)定义了一个叫$\lambda-$return的东西来定义带权的return

\[G_t^\lambda=(1-\lambda)\sum_{n=1}^\infty \lambda^{n-1}G_t^{(n)} \\ V(S_t) \leftarrow V(S_t) + \alpha (G_t^\lambda-V(S_t))\]

实际上，现在这个样子的算法复杂度还是很高的，等于还是要跑完整个episode，然后记录中间值进行融合更新。事实上，这个算法叫做forward view TD($\lambda$)，它仅仅是提供一个理论上的理解。它就像是在当前时刻，向前看，对以后时刻的return加权融合一样，然后用这个未来视角来更新当前的v。

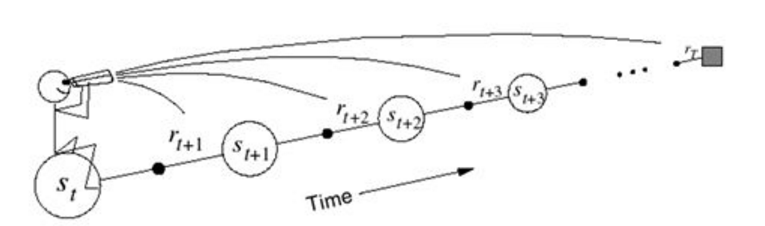
真正高效的算法是backward view TD($\lambda$)。在Backward TD($\lambda$)里，它有一个与每个状态相关联的附加内存变量，Eligibility Traces。一个状态s在时间t时候的Eligibility Trace为$E_{t}(s)$。Eligibility Traces和Hawkes Process的思维很像，用于刻画经常发生和最近发生的事件。不过Eligibility Traces的形式更加简便。如果要计算state s的Eligibility Traces，可以用下式计算。其中$1(S_{t}=s)$表示，如果第t时刻的状态是s的话取值为1，否则是0

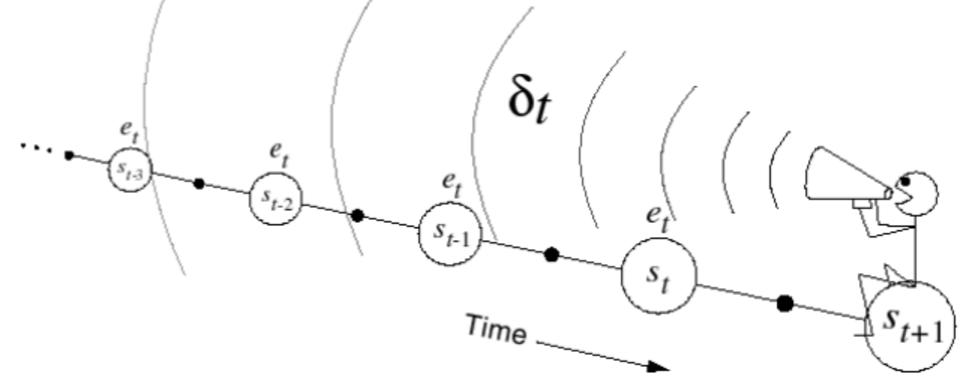
\[E_0(s)=0\\ E_{t}(s)=\gamma \lambda E_{t-1}(s) + 1(S_t=s)\]

总的来说，Eligibility Trace每个时间窗口下都在以$\gamma\lambda$缩减（因此，$\lambda$被称为trace-decay parameter），但是，如果在t时刻状态停留在s上，那么就给$E_{t}(s)$加一。它的图像如下：

结合Eligibility Traces，可以得到backward TD($\lambda$)算法的更新方式

\[\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)\\ V(s) = V(s) + \alpha \delta_tE_t(s)\]

backward TD是在当前状态下，首先计算出TD Error $\delta_{t}$，然后将TD Error回传，通知以前别的状态处的v做更新，这个更新结合了传过来的TD error和自己状态的Eligibility Traces。

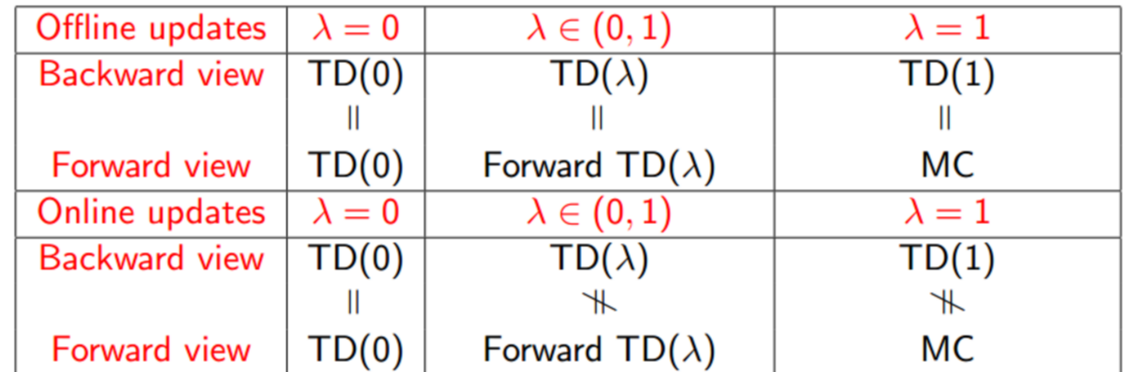
6.2.2.4 Relations MC, TD(0) and TD($\lambda$)

TD(0)=TD($\lambda$), $\lambda=0$

从算法名字就知道，TD(0)算法就是TD($\lambda$)算法在$\lambda=0$时候的特例。此时就是一次更新一个状态，因为如果$S_{t}=s$，则状态不是s的Eligibility Traces是等于0的：$E_{t}(s)=1(S_{t}=s)$。此时，对于状态s的更新就是下式，非s的不变。

\[\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)\\ V(S_t) = V(S_t) + \alpha \delta_t\]

TD($\lambda$)在offline 更新的时候，backward view = forward view

当$\lambda=1$并且TD采用offline更新的时候，TD(1)=every visit MC

6.2.2.5 Off-policy by Importance Sampling

我们同样可以采用重要性采样来计算一个return，把算法搞成off-policy的样子

\[\frac{\pi_\theta(\tau)}{\pi'(\tau)}=\frac{p(s_1) \prod_{t=1}^T \pi_\theta(a_t\mid s_t)p(s_{t+1}\mid s_t,a_t)}{p(s_1) \prod_{t=1}^T \pi'(a_t\mid s_t)p(s_{t+1}\mid s_t,a_t)} = \prod_{t=1}^T \frac{\pi_\theta(a_t\mid s_t)}{\pi'(a_t\mid s_t)}\]

这时候的更新方式就变成：

\[MC: V(S_t) \leftarrow V(S_t) + \alpha (\frac{\pi_\theta(\tau)}{\pi'(\tau)}G_t-V(S_t))\\ TD: V(S_t) \leftarrow V(S_t) +\alpha (\frac{\pi_\theta(\tau)}{\pi'(\tau)}(R_{t+1} + \gamma V(S_{t+1}) )-V(S_t))\]

6.2.2.6 Other Methods

上面说的那个方法实际上都不太适用于large MDPs，如果state或（和）action的状态空间很大，比如是个联系空间，那么上面的方法都难以处理。实际上，我们可以用一下function approximation来做，比如V(s)就是一个神经网络等等，我们转而去求解神经网络的参数就可以得到V函数。这个东西又是一个大类，将会在后续章节进行介绍。

6.2.3 Actor-critic policy gradient

在知道了怎么用critic做policy evaluation之后，就可以用actor-critic来做policy gradient啦。这里有两种方式做更新，一个是batch-based，一种是online的。

步骤中的第二个，我们可以用很多中的方式进行更新，不同的方式，就是上一章最后提到的不同的算法啦

一开始我们是通过advance function中引出actor-critic的，这种方式critic是用来评估state value function的。

\[A(s_t,a_t) \approx r(s_t,a_t)+V(s_{t+1}) - V(s_t)\]

我们当然也可以使用Eligibility Traces来展开advance function，然后带入到policy gradient里面去，得到Eligibility Traces Policy Gradient

\[\delta=R_{t+1} + \gamma V(s_{t+1})-V(s_t)\\ E_{t}(s)=\lambda E_{t}(s) + \bigtriangledown_\theta log \pi_\theta(s,a)\\ \bigtriangledown_\theta J(\theta)=E_{\tau \sim \pi_\theta(\tau)} [\bigtriangledown_\theta log \pi_\theta(\tau) \delta E]\]

其实上A还可用Q来近似，同时，critic还可以用来评估action value function。一个例子就是Q-Prop算法。

7. Extracting A Policy From Value Function

第五部分是仅仅通过actor来求解policy，第六部分的Actor-critic是通过actor和critic一起来求解最优的policy。自然而然，这一章则是仅仅通过critic来求解policy。但是与之前不同的是，本章不在通过policy gradient的方式进行求解了，而是使用贪心算法：我们通过advance function $A^\pi(s,a)$衡量了给定policy $\pi$，在状态s在，动作a比平均动作好多少，那么，我们完全可以建立一个贪心的方法，直接用advance function求解出一个至少比当前policy $\pi$更好的policy $\pi’$。

\[\pi'(a_t\mid s_t)=\left\{\begin{matrix} 1 \mbox{ if } a_t=\arg\max_{a} A^\pi(s_t, a) \\ 0 \mbox{ otherwise} \end{matrix}\right.\]

通过这种贪心迭代的方式，不断的提升policy，直至收敛。理论上来说，任何一个MDPs都会有一个最优policy，当任何状态下，走贪心步都没有policy提升的时候，就满足Bellman optimality equation了，也就达到最优了。那么，要如何最大化advance function呢？这也要取决于model是否已知

7.1 Maximum with known model

如果model已知，那么我们就可以知道状态转移等信息，那么advance function就可以写成

\[A^\pi(s,a)=Q^\pi(s,a)-V^\pi(s)=r(s,a)+\gamma E_{s' \sim P(s'\mid s,a)}[V^\pi(s')]-V^\pi(s)\]

那么，问题就转移成求V，使得policy贪心的提升：$\pi’=greedy(v_\pi)$。

7.1.1 Policy Iteration

Policy Iteration是上面问题的一种经典求解算法。具体的方法是使用$\pi’(s)=argmax_{a \in A} q_{\pi}(s,a)$，这样做是去提升，在任意状态s下的决策动作都能有提升。即在当前状态下，贪心的按照能最大化value的动作来走：

\[q_\pi(s,\pi'(s)) = max_{a \in A} q_\pi (s,a) \ge q_\pi(s, \pi(s)) = v_\pi(s)\]

致使，如果接下来的每一步都用这种贪心的方法，那么能保证走完一次后，v能有提升

\[v_\pi(s) \leq q_\pi(s, \pi'(s)) = E_{\pi'}[R_{t+1}+\gamma v_\pi(S_{t+1}) \mid S_t=s] \\ \leq E_{\pi'}[R_{t+1}+\gamma q_\pi(S_{t+1}, \pi'(S_{t+1}))\mid S_t=s]\\ \leq E_{\pi'}[R_{t+1}+\gamma R_{t+2} +\gamma q_\pi(S_{t+2}, \pi'(S_{t+2})) \mid S_t=s]\\ \leq E_{\pi'}[R_{t+1}+\gamma R_{t+2} + ... \mid S_t=s] = v_{\pi'}(s)\\\]

当贪心步骤没有提升的时候，即

\[q_\pi(s,\pi'(s)) = max_{a \in A} q_\pi (s,a)= q_\pi(s, \pi(s)) = v_\pi(s)\]

这时候就满足了Bellman optimality equation。因此，此时对于任意状态下，都有$v_\pi(s)=v_*(s)$，policy $\pi$也就是最优的了

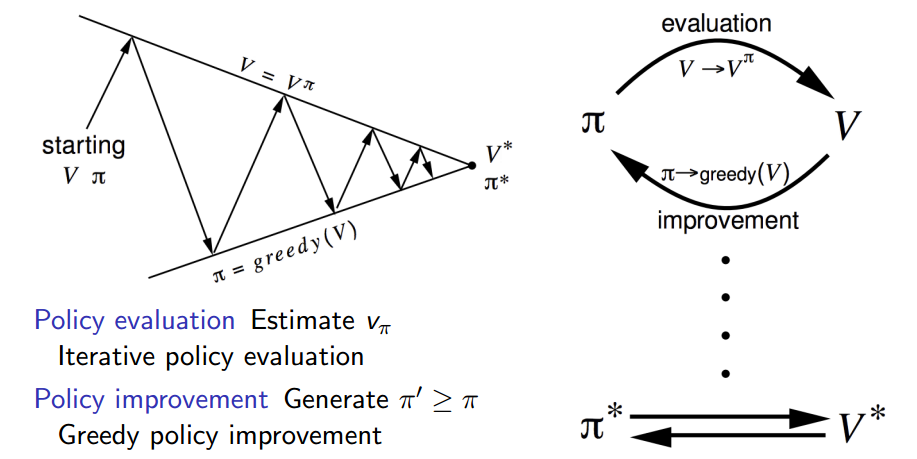
\[max_{a \in A} q_\pi (s,a)=v_\pi(s)\]

但是，问题前提是得先拿到输入变量v，也就是说在policy提升之前，我们需要先用当前policy，求出v。要求这个问题，我们可以直接使用前面说到的policy evaluation算法就可以了。所以policy iteration分成两个组成部分：policy evaluation和policy improvement，这个部分不断的迭代，直到满足最优（如下图）。

还记得上次讲policy evaluation时候的例子么

左图表示一个迭代之后的结果，也就是迭代之后的state value function。并且每一次迭代之后产生的v都能对应得到一个明确的policy（右图）。
这是policy evaluate的例子，不是iteration，也就是说，没有做policy improve。右图只是画出来的而已。实际上如果要做policy iteration，那么是在左图最后一行的结果上做的improvement（当然实际上不用迭代evaluate到这么多次）。
但事实上，右图所示的最优policy早就出现了，所以可以改进policy iteration
1. 比如，不用等到policy evaluate 收敛之后，再做policy improvement，可以设置阈值或者early stop
2. 当然，也可以每次让evaluate只做一轮迭代（k=1），这就相当于是做了value iteration。那啥是value iteration?

7.1.2 Value Iteration

回想一开始，我们的目标是贪心求解下式：

\[\pi'(a_t\mid s_t)=\left\{\begin{matrix} 1 \mbox{ if } a_t=\arg\max_{a} A^\pi(s_t, a) \\ 0 \mbox{ otherwise} \end{matrix}\right.\\ A^\pi(s,a)=Q^\pi(s,a)-V^\pi(s)=r(s,a)+\gamma E_{s' \sim P(s'\mid s,a)}[V^\pi(s')]-V^\pi(s)\]

可以看到，我们的优化目标是action a，所以直接优化Q不就好了吗？好了，这就是value iteration。

理论上来说，value iteration是建立在Principle of Optimality之上。这个定理认为任何最优的策略都由两部分组成

一个最优的首个动作a*
followed by an optimal policy from successor state S’

value iteration就是利用了这个定理。如果知道了$v_\star(s’)$那么他的前一步最优状态$v_\star(s)$也就可以通过Bellman optimality equation而知道了。

\[v_*(s) =\max_{a\in A} \left( R_s^a + \gamma \sum_{s' \in S} P^a_{ss'}v_*(s') \right)\]

其中，$P_{ss’}^a=P(s’\mid s, a)$。所以，value iteration就不断的迭代这个式子，也就是在max Q：

\[v_{k+1}(s) =\max_{a\in A} \left(R_s^a + \gamma \sum_{s' \in S} P^a_{ss'}v_k(s') \right)\\ \mbox{也就是说去迭代：} Q(s,a) = r(s,a) + \gamma E_{P_{ss'}^a}[V(s')]\\ V(s) = max_a Q(s,a)\]

最后最优的policy则可以用下式给出：

\[\pi_*(s)=\arg\max_{a \in A} \left( R_{s}^a + \gamma \sum_{s' \in S}P^a_{ss'} v_*(s')\right)\]

Policy iteration V.S. Value iterataion

value iteration是两步组成：找最优$v_\star$，得到最优$\pi_{\star}$，而policy iteration是一个loop，不断的优化v和$\pi$。这说明了value iteration之所以不迭代，是直接找到了最优的v，它对应的策略也自然是最优的
对于value iteration找最优的v的过程，可以看做是特殊的policy iteration：（k=1的policy evaluate + policy improve的组合），难道只是思想上的相同？？value iteration是用max做一次v的sweep
policy iteration的不好之处就是有太多次的policy evaluate，而且每一次都针对所有的状态做更新v(s)（即v_{k+1} -> v_{k}）。所以才会提出value iteration。
两者的复杂度都是很高的！他们都是建立在优化v上，这就意味着每一次迭代有$O(mn^2)$的复杂度。其中m是actions，n是states（给定一个状态，首先遍历m个动作，然后分别能跳转到n个新状态下。这个操作对每个state都得跑一次，所以还得乘一个n，也就是mn^2）

对于这种巨大的state开销，v函数往往也可以用一个其他模型代替，比如训练一个神经网络，参数是$\phi$，输入是state s，输出V(s)

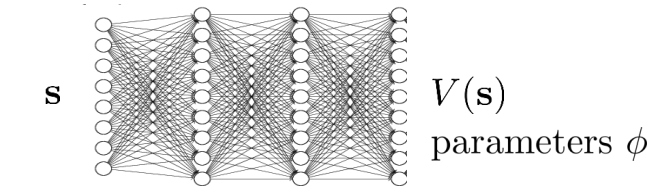
那么，我们可以得到一个新的框架：Fitted value iteration。这个算法框架是用一个模型近似$V_\phi(s)$，比如最小化Bellman optimality loss

\[L(\phi)=\frac{1}{2} \mid \mid V_\phi(s) - \max_a Q(s,a) \mid \mid_2^2\]

这时候的迭代方法就稍微有一点点改变：

7.2 Maximum with unkown model

上文提到的求解方法，包括policy iteration和value iteration，都是建立在state value function之上的。但是他们都涉及到了$E_{P_{ss’}^a}[V(s’)]$，需要我们已知dynamics，知道状态转移P。这在实际问题中，是很不现实的。并且，在unknown model的情况下，就算我们能通过dynamics-free的方式求出state value function，我们也不知道在某个状态下到底应该怎么出action才能最大化reward，因为并不知道状态转移P。

\[\pi'(s)=\arg\max_{a} R^a_s + P^a_{ss'} V(s')\]

因此，用state value function V做policy improvement需要知道MDPs，但是，用action value function Q来做的话就是model-free的！因为Q是关于state和action的函数，知道Q的话，我们就知道在state上怎么做action才会更好，也就可以得到policy

\[\pi'(s)=\arg\max_{a} Q(s,a)\]

那么，我们把之前policy iteration和value iteration的那一套流程，改作在Q上。

\[Q^\pi(s,a) = r(s,a) + \gamma E_{s' \sim P^a_{ss'}} [Q^\pi(s', \pi(s'))]\]

由于model是不知道的，所以，我们可以把policy evaluetion with unkown MDPs的方法作用在Q上。在得到Q之后，就可以贪心的求解policy。

\[\pi'(a_t\mid s_t)=\left\{\begin{matrix} 1 \mbox{ if } a_t=\arg\max_{a} Q^\pi(s_t, a) \\ 0 \mbox{ otherwise} \end{matrix}\right.\]

但是，在求解Q的过程中，我们是采用policy evaluetion with unkown MDPs，这是依赖于样本的操作。如果发现一个Q，在某个state上做一个action效果比较好的话，我们学到的策略就会一直做这个动作。但是，通过MC来找出的Q，难以有泛化性能（仅仅对已经经历过的状态做出决策），所以往往不能依靠建立在Q上的贪心策略，action不一定是最优的。所以，这时候会采用$\epsilon-greedy$方法（m是action的总个数）：以一定概率取当前贪心步，或者等概率的取其他步。

\[\pi(a\mid s)=\left\{\begin{matrix} \epsilon /m + 1 - \epsilon \mbox{ if } a^*=\arg\max_{a \in A} Q(s,a) \\ \epsilon /m \mbox{ otherwise } \end{matrix}\right.\]

当然，这个策略也是能保证对策略有提升的，一般来说$\epsilon_{k}=\frac{1}{k}$，这样满足Greedy in the Limit with Infinite Exploration (GLIE) 的条件。

7.2.1 policy evaluetion on Q with MC

这个方法和on V的MC类似，只是统计量不同啦

on V

\[N(S_t) += 1 \\ V(S_t) \leftarrow V(S_t) + \frac{1}{N(S_{t})} (G_t -V(S_t))\]

on Q

\[N(S_t, A_t) += 1 \\ Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \frac{1}{N(S_{t}, A_t)} (G_t -Q(S_t, A_t))\]

7.2.2 policy evaluetion on Q with TD

使用TD的原因，和on V的TD原因也是类似的。比如TD可以做online，低方差等等

on V

\[V(S_t) \leftarrow V(S_t) +\alpha (R_{t+1} + \gamma V(S_{t+1}) -V(S_t))\]

on Q

\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) +\alpha (R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) -Q(S_t, A_t))\]

值得一提的是，on Q的这个算法被称为Sarsa，因为他从一个状态动作对(s,a)，经过一个reward r，转移到另一个状态动作对(s’,a’)了。下面是sarsa的伪代码

7.2.3 policy evaluetion on Q with n-step Sarsa & Sarsa($\lambda$)

这个和on V的n-step TD和 TD($\lambda$)也是类似的。定义n-step Q-return和更新方法

\[q_t^n = R_{t+1} + \gamma R_{t+2} + ... \gamma ^{n-1} R_{t+n} + \gamma^n Q(S_{t+n})\\ Q(S_t, A_t) \leftarrow Q(S_t, A_t) +\alpha (q_t^n -Q(S_t, A_t))\]

Forward view Sarsa($\lambda$)

\[q_t^\lambda=(1-\lambda)\sum_{n=1}^\infty \lambda^{n-1}q_t^{n} \\ Q(S_t, A_t) \leftarrow Q(S_t, A_t) +\alpha (q_t^\lambda -Q(S_t, A_t))\]

Backward view Sarsa($\lambda$) with Eligibility trace

\[E_0(s,a)=0\\ E_{t}(s,a)=\gamma \lambda E_{t-1}(s,a) + 1(S_t=s, A_t=a)\\ \delta_t = R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)\\ Q(s,a) = Q(s,a) + \alpha \delta_tE_t(s,a)\]

下图是Sarsa($\lambda$) 的代码

7.2.3 Off-policy evaluation: Q-Learning

首先需要说明的是，我们可以用importance sampling的方式来做Q，就像在之前用他来做V一样，这里就略去咯。下文是解释Q-learning，它是一个脱离importance sampling框架的东西

回想之前的fitted value iteration，他是去求解V

现在我们把他改成求解Q。我们可以通过下式建立他们之间的联系

\[Q(s_t, a_t)=r(s_t,a_t)+\gamma E_{s' \sim P_{s_ts_{t+1}}^{a_t}}[V(s_{t+1})]\]

也就是说，把fitted value iteration的第一步改成最大化上式的等式右端，第二版改成用y来近似等式左端。加入我们的采样步骤，就可以得到fitted Q iteration，其中K表示mini-batch的大小。

当k=1的时候，就是online Q-iteration了

这里的Q也可以用一个神经网络来代替

对于online Q-iteration的更常见一种叫法是Q-Learning。另外，我们还可以把Q-Learning的形式写成下面这个样子。这就和之前提到的Sarsa算法很像咯。但是Sarsa是on-policy的，Q-learning是off-policy的（可以吧Q-learning的behavior policy看成是在Q下的贪心policy，即式子中max的那一项。如此，在Q-learning中target policy和behavior policy都一起有了提升）。

\[Q-Learing: Q(S_t, A_t) \leftarrow Q(S_t, A_t) +\alpha (R_{t+1} + \gamma \max_{a_{t+1}}Q(S_{t+1}, a_{t+1}) -Q(S_t, A_t))\\ Sarsa: Q(S_t, A_t) \leftarrow Q(S_t, A_t) +\alpha (R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) -Q(S_t, A_t))\]

总的来说，Q-iteration这种求解方式实际上是在优化一个近似的Bellman optimality loss，对于Bellman optimality equation for Q来说，满足

\[q_*(s,a) = R_s^a + \gamma \sum_{s' \in S} P_{ss'}^a \max_a’ q_*(s',a')\]

而Q-iteration采用的是近似策略：

\[loss = q_*(s,a) - ( R_s^a + \gamma \max_a’ q_*(s',a'))\]

从理论上来说，这种迭代求解方式在离散state和action的情况下（Q能表示成一个tabular），是能保证policy improvement。当loss=0的时候，就达到最优的Q了。但是，除此之外，是不能保证这个性质的。所以，在实际使用Q-learning的时候，会有很多新的算法trick。

7.3 Value function learning theory

首先一个大结论就是：value iteration在tabular的情况下是保证收敛的，但是fitted value iteration往往是在任何情况下，都不收敛的。以Q-learning/online Q iteration为例，他的算法流程如下

他的更新方法，完全就可以下次下面这gradient descent的形式

\[\phi \leftarrow \phi - \alpha \frac{dQ_\phi(s_i,a_i)}{d\phi}\left(Q_\phi(s_i,a_i) - [r(s_i,a_i) + \gamma \max_{a'}Q_\phi(s'_i,a'_i)]\right)\]

但是它其实不是一个gradient descent，所以保证不了像gradient descent收敛的结论。原因是每一个迭代更新了参数$\phi$之后，Q也被更新了，使得y（称为Q-target）也就变了，算法拟合的目标也变了。实际上，使用非线性方法近似value function的话，很多情况下都不能保证收敛的。

8. Advanced Q-Learning with Function Approximation

前文的Q-learning在实际使用中有太多的问题，效果通常很不稳定。本文主要从Deep reinforcement learning的角度，介绍一些trick和模型。这些模型的建立背景是使用其他的函数或者模型来近似policy或者value。比如使用神经网络来近似Q或者近似$\pi$。

8.1 Function Approximation

8.1.1 Why Function Approximation

对于V函数来说，我们需要维护一个从State到V(S)的映射表；对于Q函数来说，我们要维护一个从state和action到Q(s,a)的映射表，甚至对于policy来说，我们还需要一个从state到action的映射表。当state和action的空间很大的时候（Large MDPs），维护这些是很费内存空间的。
当我们使用样本来应对model-free问题的时候，采样样本很可能无法覆盖这个state或者action的空间，那么，这时候学习出来的映射表对于没有出现过的state或者action就无法给出决策。缺乏generalization

所以，我们希望通过Function Approximation的方式来近似这些映射表，应对large MDPs的同时，扩展generalization。具体来说，function approximation达到的目的是用一个函数来近似V，或者(和)Q，或者（和）policy。下式我们用$\phi$来统一指代function approximation中的参数（并不是表示三者共享一个参数的意思）。

\[V_\phi(s) \approx V_\pi(s)\\ Q_\phi(s,a) \approx Q_\pi(s,a)\\ \pi_\phi(a\mid s) \approx \pi(a\mid s)\]

比如我们使用一个黑箱模型来近似V，Q。当然这个策略不一定是单输出的。比如图三，给定一个state，它可以把所有action的Q都输出。

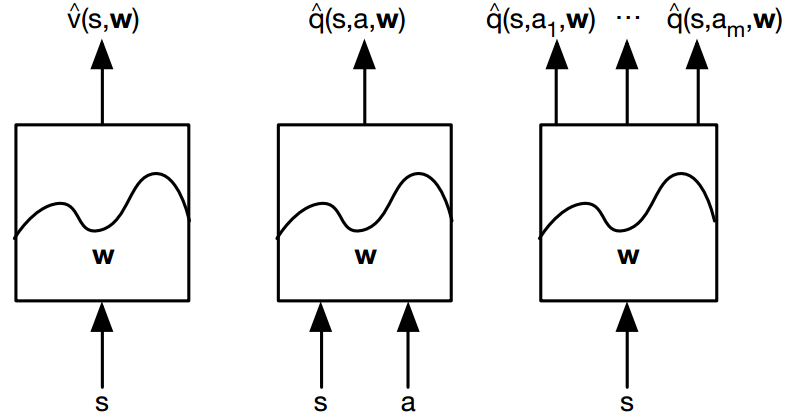
给定function的形式之后，对V，Q，$\pi$的求解就变成了对参数$\phi$的求解（回想一下，我们在讲policy gradient，Fitted Q-iteration的时候就是这么干的）。那么，可以选择哪些function来做approximate呢？其实都可以，只要模型能处理episode，并且你有能力解得出来就行。但是这也是一个function表达能力与复杂度的trade off：要知道，V，Q，$\pi$本身的选择空间是比较大的，如果选用的function的表达能力太弱，那么效果就自然不用多说了。表达能力强的往往复杂度太高，求解不太容易。但是，Deep Reinforcement Learning（用Deep Network来做function approximation）却是一个大热的方向。当然，也可以使用线性模型来做。

8.1.2 Policy evaluation with function approximation

前面我们介绍了在dynamics已知和未知，两种情况下去求解Q和V函数。现在我们使用function approximation来求解参数。如果没有特别指明，下文都采用线性模型来做近似（如下图），其中函数$f(X)$表示对X取特征（比如，$f(S)$表示state的特征向量）

\[V_\phi(S)=f(S)^T\phi \mbox{ } \mbox{ } \mbox{ } \mbox{ } \mbox{ } Q_\phi(S,A)=f(S,A)^T\phi\]

8.1.2.1 Approximating state value function

首先，我们总结一下对于V函数的policy evaluetion是怎么做的

\[\mbox{MC：} V(S_t) \leftarrow V(S_t) +\alpha (G_t -V(S_t))\\ \mbox{TD：} V(S_t) \leftarrow V(S_t) +\alpha (R_{t+1} + \gamma V(S_{t+1}) -V(S_t))\\ \mbox{N-step TD：} V(S_t) \leftarrow V(S_t) +\alpha (G_t^n -V(S_t))\\ \mbox{forward TD(lambda)：} V(S_t) \leftarrow V(S_t) + \alpha (G_t^\lambda-V(S_t))\\ \mbox{backward TD(lambda)：}V(s) = V(s) + \alpha \delta_tE_t(s)\\ E_{t}(s)=\gamma \lambda E_{t-1}(s) + 1(S_t=s)\\ \delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)\\\]

以上的流程需要维护一个$S \rightarrow V(S)$的tabular，每次用右端的值更新左端的时候，都涉及到查表的操作，然后为每一个state做更新。现在，我们需要用$V_\phi$来近似$V$，尽量的缩小让两者差距。那么，我们可以去最小化差距就行了，比如最小化相差的二范数：

\[J(\phi)=E_\pi\left[ (V_\phi(S) - V(S))^2 \right]\]

有了目标函数，我们就可以用policy gradient的思想，用gradient来最小化上面的loss

\[\triangledown_\phi J(\phi)=(V_\phi(S)-V(S))f(S)\\ \phi \leftarrow \phi - \alpha \triangledown_\phi J(\phi)\]

注意，公式里的$V(S)$是未知的。这个问题可以借鉴之前，V函数的policy evaluetion的思路，使用样本来近似他。所以：

\[\mbox{MC：}\triangledown_\phi J(\phi)=(V_\phi(S_t)-G_t)f(S_t)\\ \mbox{TD：}\triangledown_\phi J(\phi)=(V_\phi(S_t)-(R_{t+1} + \gamma V_\phi(S_{t+1})))f(S_t)\\ \mbox{Forward TD(lambda)：}\triangledown_\phi J(\phi)=(V_\phi(S_t)-G_t^\lambda)f(S_t)\\ \mbox{Backward TD(lambda)：}\triangledown_\phi J(\phi)=\delta_tE_t\\ \delta_t= V_\phi(S_t)-R_{t+1} + \gamma V_\phi(S_{t+1})\\ E_t=\gamma \lambda E_{t-1}+f(S_t)\]

8.1.2.2 Approximating action value function

借用上一节的想法，我们也可以对Q函数建立以下的优化目标（这里我还是假设使用L2损失）

\[J(\phi)=E_\pi\left[ (q_\phi(S,A)-q(S,A))^2 \right]\]

同理，我们可以得到更新式子：

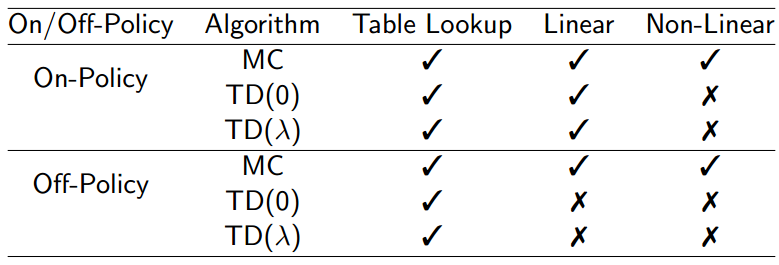
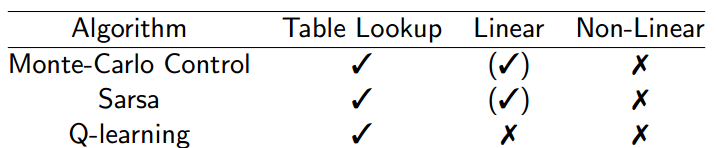
\[\mbox{MC：}\triangledown_\phi J(\phi)=(q_\phi(S_t,A_t)-G_t)f(S_t,A_t)\\ \mbox{TD：}\triangledown_\phi J(\phi)=(q_\phi(S_t,A_t)-(R_{t+1} + \gamma q_\phi(S_{t+1},A_{t+1})))f(S_t,A_t) \\ \mbox{Forward TD(lambda)：}\triangledown_\phi J(\phi)=(q_\phi(S_t,A_t)-G_t^\lambda)f(S_t,A_t)\\ \mbox{Backward TD(lambda)：}\triangledown_\phi J(\phi)=\delta_tE_t\\ \delta_t= q_\phi(S_t,A_t)-R_{t+1} + \gamma q_\phi(S_{t+1} ,A_{t+1} )\\ E_t=\gamma \lambda E_{t-1}+f(S_t,A_t)\]

还有一个需要注意的问题。在Q-learning部分，我们已经提及function approximation的收敛性问题，下图是一个关于function approximation做policy evaluation更全的总结。打钩的表示能收敛到optimal。括号加钩表示near-optimal。第一个图是做prediction时候的结论。第二个图是做control时候的结果。

8.2 Advanced Q-Learning with Deep Network

现在开始介绍一些在Deep Network上的一些trick，来保证Q-Learning效果的稳定性。对于Q-Learning来说，他的更新式子如下。$Q_\phi$是一个神经网络，用来近似求解Q函数，目标函数由近似的Bellman optimality loss给定。

\[\phi \leftarrow \phi - \alpha \frac{dQ_\phi(s_i,a_i)}{d\phi}\left(Q_\phi(s_i,a_i) - [r(s_i,a_i) + \gamma \max_{a'}Q_\phi(s'_i,a'_i)]\right)\]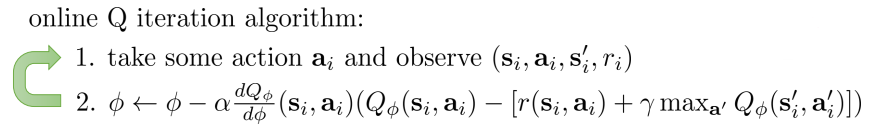

在某个状态s上，Q-learning首先根据当前策略，做出动作a，然后收到environment的反馈信息r和新的状态s’。也就说，Q-Learning的训练数据是$\left[ (s_{1},a_{1}, s_{2},r_{2}),(s_{2},a_{2}, s_{3},r_{3}),…,(s_{T-1},a_{T-1}, s_{T},r_{T}) \right]^N$。可以看到，在一条episode中的数据是高度相关的。这会导致在episode中的local overfit。这是Q-Learning效果不稳定原因之一。另一方面，和之前提到的一样：Q-Learning的更新方式不是gradient descent，所以保证不了像gradient descent收敛的结论。原因是每一个迭代更新了参数$\phi$之后，Q也被更新了，使得Q-target y也就跟着变了，算法拟合的目标也就变了。

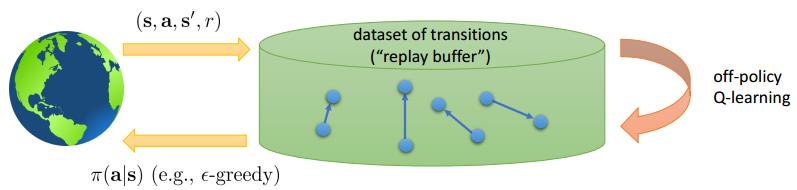
超级经典的DQN算法就是针对这两点问题做出了改进，取得了一大进步（当然，现在的DQN只能作为一种baseline，被各大论文虐杀）。DQN效果通过两招得以保证：Experience Replay（也可以叫replay buffers）和fixed Q-target。这两招在其他论文/算法中也被经常使用。

8.2.1 Experience replay to reduce sample correlation

为了打破优化过程中的样本依赖，experience replay维护了一部分历史信息，称为experience，然后每次从experience中抽样（这样就打破依赖啦），喂给Q-learning的更新式子，所以叫做experience replay。experience replay用了一个buffer来存储experience（如下）：

整体的流程是：

给定s，根据当前策略，做出动作a，得到environment的反馈信息
将四元组$(s_{t},a_{t}, s_{t+1},r_{t+1})$放入buffer中（如果buffer满了，就覆盖老的数据）
从buffer中采样一个四元组或者mini-batch的四元组，用这些数据来做当前轮的更新。整个过程就是off-policy的啦

8.2.2 Fixed Q-target to stabilize gradient

Q-learning效果不稳定的另一个原因就是Q-target老是在变。Fixed Q-target要做的，顾名思义，就是在做更新的时候把Q-target给固定住。为了固定Q-target，这里引入了两套参数（也就对应两个网络）来学习Q。即，原始目标：

\[E\left[Q_\phi(s_i,a_i) - [r(s_i,a_i) + \gamma \max_{a'}Q_\phi(s'_i,a'_i)]\right]\]

变成由两个参数（$\phi1,\phi2$）对应的网络来学习：在学习$\phi1$的时候，用$\phi2$来代表Q-target

\[E\left[Q_{\phi1}(s_i,a_i) - [r(s_i,a_i) + \gamma \max_{a'}Q_{\phi2}(s'_i,a'_i)]\right]\]

在迭代学习K次之后，令$\phi2=\phi1$。综合experience replay和fixed q-target，下面给出DQN的伪代码：

8.2.3 Polyak-style averaging

在Fixed Q-learning里面，如果第t时刻，我们将$\phi2=\phi1$，然后

第t+1时刻，DQN相当于是使用t时刻的参数拟合Q-target，然后去更新t+1时刻的参数
第t+2时刻，DQN相当于是使用t时刻的参数拟合Q-target，然后去更新t+2时刻的参数
第t+N时刻，DQN相当于是使用t时刻的参数拟合Q-target，然后去更新t+N时刻的参数

用图说话就是：

可以看到，箭头的长度是不一样的，Polyak-style averaging就是要解决这样“不公平”的现象，使得用相等间隔大小下的Q-target去做参数更新。实现方式很简单，仅仅是改变了赋值方式（下式）。传说可以取经验值$\beta=0.999$

\[\phi2 = \beta \phi1 + (1-\beta)\phi1\]

8.2.4 Double Q-Learning to avoid overestimate Q

DQN另一个问题就是，所学习出来的Q和真实的Q值之间的差距太大。一旦Q的值过大，就会使得最后return的值也变大。下图是在不同数据集下所学习出来的效果曲线，其中红色曲线就是DQN的结果，红色横线是真实的结果。为了解决这个问题，double DQN被提了出来，图中，蓝色曲线就是double DQN的结果，蓝色横线是double DQN的真实结果。

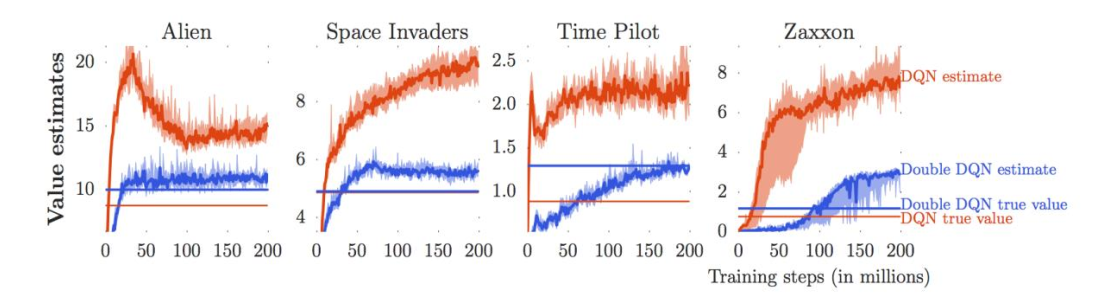
DQN（Q-Learning）对Q的估计值过大的问题，Q target中的max造成的。

\[\mbox{Q target: }r(s_i,a_i) + \gamma \max_{a'}Q_\phi(s'_i,a'_i)\]

由于$Q_\phi$对Q的估计可能不准确（尤其是一开始的时候），使得$Q_\phi$约等于是真实Q加上noise。如果在某个状态下，本应该选择action a，但是由于$Q_\phi$的估计不准，选择了当前它认为的最好action a’ （by $\max_{a’}Q_\phi(s’{i},a’{i})$）。这种错误的选择，会随着迭代进一步放大，最后学到的policy可能就不是最优的了。所以，必须要解决这种overestimation Q的问题。我们现在把max那项写成下式：

\[\max_{a'}Q_\phi(s'_i,a'_i)= Q_\phi(s'_i, \arg\max_{a'}Q_\phi(s'_i,a'_i))\]

上式表明，Q-learning是使用$Q_\phi$来选择action，也用它来评估了value function。这样的话自然会选择有max positive noise的动作。Double Q-learning就是通过解耦这两个地方来解决overestimate的问题。也就是说，选action和评估value function使用不同的Q approximations来做！这样，就算两个Q approximation都有noise，但是这两个noise是不太相关的，所以问题就解决了。

下图是Double Q-learning的代码。这里有两个 Q approximation: Q1和Q2，他们分别用对方来做评估，用自己来选动作。

这个过程感觉和fixed Q-learning有一点点像，但是这里并没有参数的copy，并且Q1和Q2也可以是完全不同的网络。

8.2.5 N-step return to reduce variance

我们同样可以把Q target做扩展到N-step下，这个扩展就与TD target中的N-step TD target很类似了。这里就不再展开了

8.2.6 Continuous actions extension

在Q-Learning里最可怕的就是Q target中$\max_{a’}Q_\phi(s’{i}, a’{i})$ 的求解了，而且是每次迭代都得求解一下。如果我们的action空间是离散的，那么我们可以遍历一下，选出最好。但是，如果我们的action空间是连续的（或者离散空间超级大的时候），这个求解就很烦人了。当然，我们可以使用Gradient Descent等等方式进行求解，但是在每次迭代中再嵌套一个迭代，实在是慢上慢。下面，介绍一些其他可选的方案

8.2.6.1 Stochastic optimization

梯度下降的方式迭代太多太慢，那么可以试试随机优化的策略。他的思想在于首先从均匀分布中对action进行采样$(a_{1},…,a_{N})$，然后看看哪个的$Q(s,a_{i})$大，就选哪个action。这种策略叫做random shooting。该方法简单，效率很高，唯一的缺陷就是准确度不高。另一个改进算法就是使用cross-entropy method（CEM），它是一种iterative stochastic optimization。CEM首先某个分布p中采样N个action，然后看看他们的Q值是多少，然后选择前K个Q大的action，用他们来改进采样分布p。

8.2.6.2 Choose $Q_\phi$ carefully

直观的说，一开始选一个容易求解最大值的$Q_\phi$不就好了吗？恩，Normalized Advantage Functions（NAF）就是这么做的。NAF选择的$Q_\phi$是：

\[Q_\phi(s,a)=-\frac{1}{2}(a - \mu_\phi(s)^T)P_\phi(s)(a-\mu_\phi(s)) + V_\phi(s)\]

这样，它直接在$a=\mu_\phi(s)$的时候，取到最大值$V_\phi(s)$。确点就是模型的表达能力不行

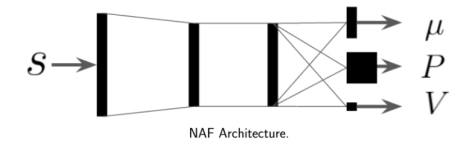
8.2.6.3 Learn an approximate maximizer

最后一个手段：既然求max很难，那为何不学习出一个网络$\mu_\theta(s)$，让它来近似Q取最大值时候的action，也就是说：

\[\mu_\theta(s) \approx \arg\max_a Q_\phi(s,a)\]

Deep deterministic policy gradient (DDPG)就是这么做的。这样，又可以通过梯度来进行求解咯

\[\theta = \arg\max_\theta Q_\phi(s, \mu_\theta(s)) \mbox{ } \rightarrow\mbox{ }\mbox{ } \frac{dQ_\phi}{d\theta}=\frac{da}{d\theta}\frac{Q_\phi}{da}\]

下图就是DDPG的伪代码啦。DDPG需要对Q网络和maximizer同时更新，代码里的B就是replay buffer。

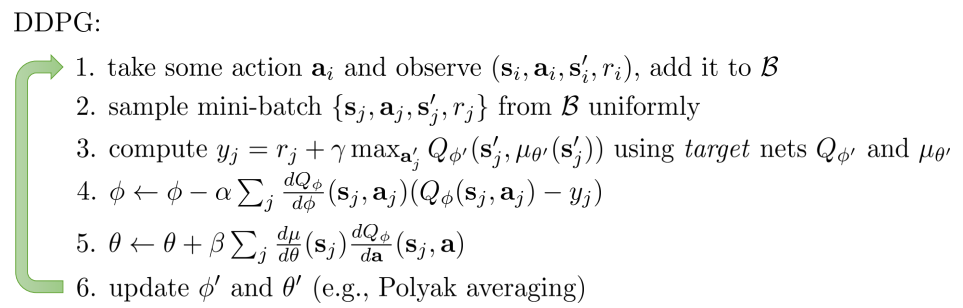
9. Model-based Planning

之前的几个部分，我们提到了policy-based和value-based都是在dynamics未知的时候给出的算法，要是环境的dynamics已知（好比如知道对方怎么出招），那么，对于policy的求解讲变得更加容易（见招拆招）。实际上，在policy evaluation部分，policy iteration和value iteration两类算法就是建立在transition dynamics已知的情况下的。在dynamics已知的情况下，agent不通过与环境的真实交互，利用这个dynamics来生成或者提升policy。这种操作就叫planning。比如，AlphaGo的蒙特卡洛树搜索就是一种planning。再比如打羽毛球的时候，根据有木有风，球的速度角度等来估计球的落点，然后跑过去接球，这也是一个planning。

planning的方式有很多，policy evaluation是通过动态规划的方式来做的planning，AlphaGo是通过tree search的方式来做的planning。需要注意的是，在做planning的时候，不一定要和environment做交互。如果每个决策都和environment交互，就对应下面左图的closed loop。但是在给定dynamics之后，当environment告诉我们所处的状态，我们就可以做出一个动作序列（因为我已经知道，如果第t时刻我做a，我会被转到s下，那么我就可以直接估计第t+1时刻的动作了，以此类推），不再进行交互了，对于右图的open-loop。

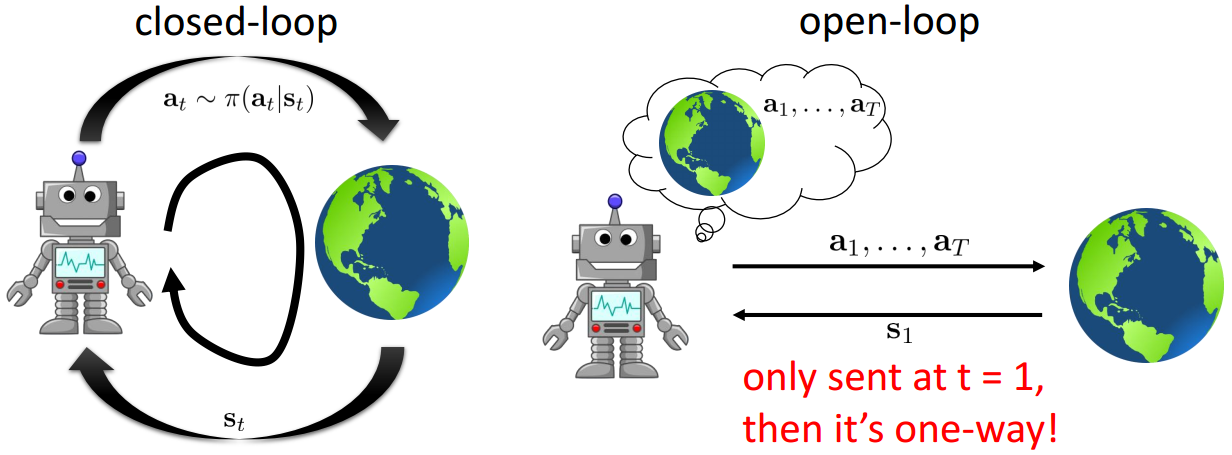
对于closed loop来说，我们需要最大化下式

\[\pi=\arg\max_\pi E_{\tau \sim p(\tau)}\left[ \sum_t \gamma^{t-1} r(s_t,a_t) \right]\]

对于open loop来说，我们一次性可以得到一个动作序列

\[a_1,...,a_T=\arg\max_{a_1,...,a_T} E_{\tau \sim p(\tau)}\left[ \sum_t \gamma^{t-1} r(s_t,a_t) | a_1,...,a_T\right]\]

对于第二种来说，这有点像deterministic policy（只是长得像）。所谓的deterministic policy是说输入一个state，只能输出一个动作，而对应的Stochastic policy，它是输出一个动作的分布，每次选取有可能选不到概率最大的action。对于open loop来说，即便是已知dynamics，planning出来的结果可能是次优的。因为planning得越远，可能产生的误差越大，最好的情况当然是交互式的。本章节，将对planning的方法做一些介绍。当然了，policy evaluation就不再赘述了。

9.1 Stochastic optimization

随机优化这种方式仅仅适用于open loop的条件，他和我们之前说到的随机优化的方式类似，只是这里目标变量变成高维的了。我们要求的就是一个高维的action

\[a_1,...,a_T=\arg\max_{a_1,...,a_T}J( a_1,...,a_T)\]

但是这种方式在维度太高的时候，效果其实很一般。也就是说不适用于去plan很久远的future，短期的plan会很work

9.2 Monte Carlo tree search (MCTS)

MCTS是在AlphaGo里面用到的方法，他是一种基于树形结构的前向搜索算法，树的节点表示状态。这句话的意思就是，给定当前状态$S_{t}$，以$S_{t}$为根节点建立一棵树向下展开，通过遍历动作空间的取值，跳转到新的状态，依次类推。MCTS并不会就MDP中所有可能的状态都建立成一个大树，而是仅仅为当前时刻下的状态建立一个“子树”。对于子树中的每一个节点（状态），MCTS都会去评估他的value function，以便于在当前时刻下的状态$S_{t}$做出决策动作。当然这颗子树也不会一直展开下去，展开到一定程度之后，将停止展开。对于非叶子节点，在子树展开的过程中就在不断的评估他们的value function，这个展开子树的策略叫做tree policy，而对叶子节点进行评估的policy叫做default policy，一般default policy是一个random policy，也就是下图中的波浪线部分。

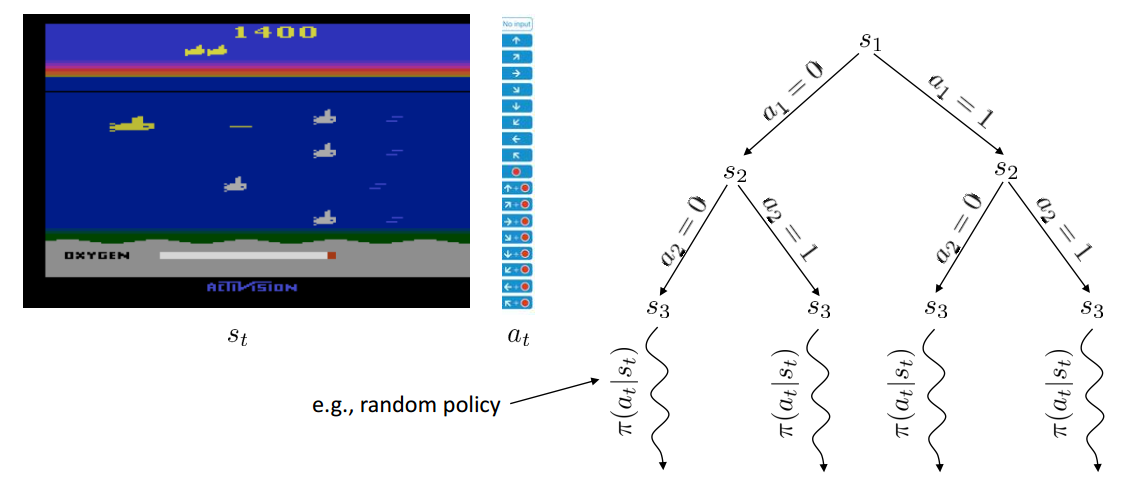
default policy的评估肯定是不精确的，但是这种不精确是与时间复杂度之间的trade-off。从AlphaGo的效果来看，这个不精确带来的误差也是挺小的。下图是MCTS的一个算法框架（这个算法伪代码是和上图联系起来的，并不是说一定要从s1开始，准确的说，应该是从当前时刻t开始）：

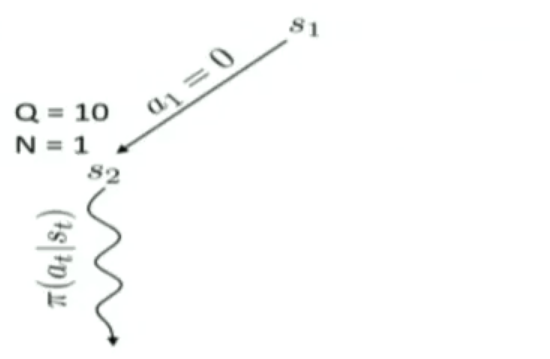
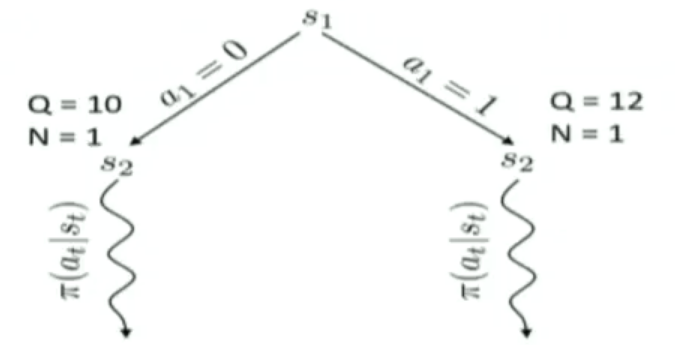
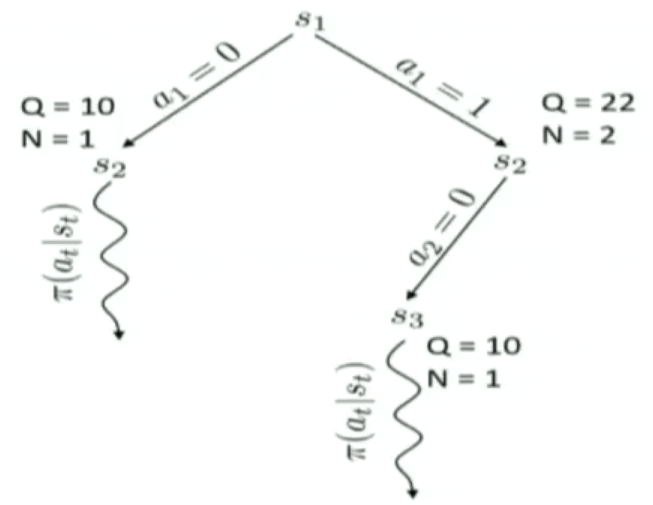
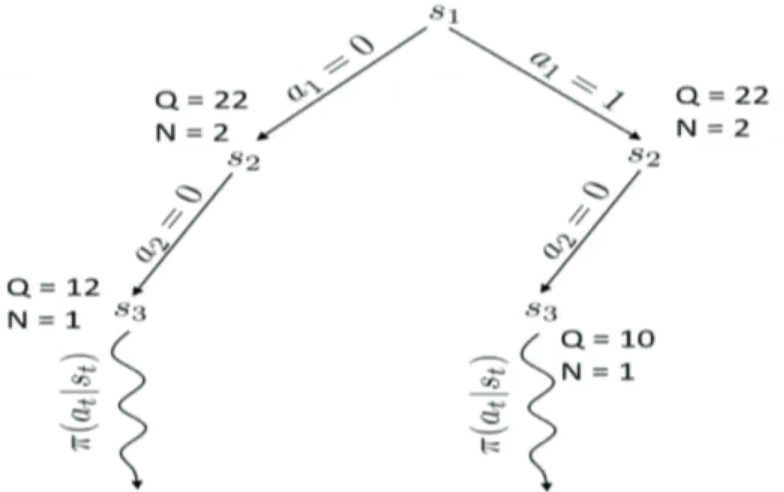
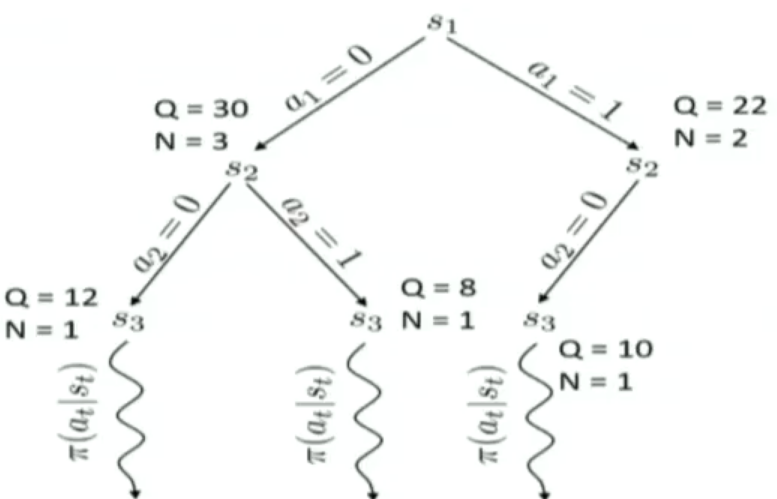
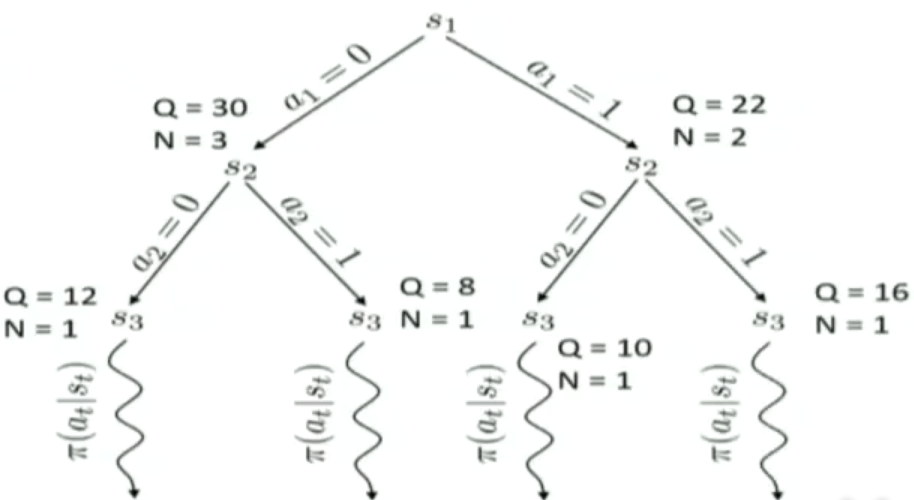
Tree policy并不是直接就遍历整个action space了，而是1）首先选择一个没有选过的action；2）如果action都被访问过了，那么就选择一个最好的action走。这里“最好的action”是指按照这个action，会走到一个得分最高的state上。这里state的得分计算公式是一个Upper Confidence Bounds（UCB）。它长成下面这个样子。其中$Fa(s)$表示节点s的父节点，$N(s)$表示节点s被访问过的次数，$Q(s)$，对于叶子节点来说，是它的return（是MC采样得到的？），对于非叶子来说，表示所以孩子节点的Q的和

\[Score(s)=\frac{Q(s)}{N(s)} + 2C \sqrt{\frac{2 ln N(Fa(s))}{N(s)}}\]

这个过程可以用下图表示

9.3 Trajectory optimization

9.3.1 Linear dynamics case

最后一种，是最直接也是公式最多的一招，旨在直接去针对trajectory优化整个planning的过程。他的优化目标是下式，这里的函数$f$代表了dynamics。给定当前时刻的状态和action，并且已知dynamics，那么下一个时刻的状态我就知道了，既然知道了新状态，我当然也就能给出新动作。因此trajectory optimization就是要找出一个能最小化cost（最大化reward）的trajectory：

\[\min_{a_1,... ,a_T} \sum_{t=1}^T c(s_t,a_t) \mbox{ s.t. } s_t=f(s_{t-1},a_{t-1})\\ \min_{a_1,... ,a_T} c(s_1,a_1) + c(f(s_1,a_1),a_2)+...+c(f(f(...)),a_T)\]

优化上面的问题，可以采用求导的方式进行backpropagation。其中一个经典的算法就是linear quadratic regulator（LQR），他用来处理当dynamics是线性，cost（可以看出是negative reward）是二次的情况。简单的说，它假设c和f函数符合下面的函数形式（f是linear，c是quadratic）：

\[f(s_t,a_t)=F_t\begin{bmatrix} s_t \\ a_t \end{bmatrix} + f_t\\ c(s_t,a_t)=\frac{1}{2}\begin{bmatrix} s_t \\ a_t \end{bmatrix} ^T C_t \begin{bmatrix} s_t \\ a_t \end{bmatrix} +\begin{bmatrix} s_t \\ a_t \end{bmatrix} ^T c_t\]

由于这个算法设计到的数学推导太多，这里就只简单说说他的优化策略。总的来说，LQR是逆序优化的，它首先求解$a_{T}$，因为$a_{T}$仅仅依赖$s_{T}$，所以，$a_{T}$可以用$s_{T}$完全表示出来，同理，LQR用$a_{T-1}$可以用$s_{T}$完全表示，直到表示到$s_{1}$。这里的$s_{1}$正是在open loop的时候，环境给我们的信息。然后我们用这个信息再反带回到$a_{T}$上，也就得到了一个action的序列了。具体的公式推导，有兴趣的请自行查阅。

首先对$a_{T}$的求解，是通过对最后一项求导得到的：

\[a_T=K_Ts_T+k_T\\ K_T=-C^{-1}_{a_T,a_T}C_{a_T,s_T}\\ k_T=-C^{-1}_{a_T,a_T}c_{a_T}\\ C_T=\begin{bmatrix} C_{s_T,s_T} & C_{s_T,a_T} \\ C_{a_T,s_T} & C_{a_T,a_T} \end{bmatrix}\\ c_T=\begin{bmatrix} c_{s_T} \\ c_{a_T} \end{bmatrix}\]

$a_{T}$可以用$s_{T}$完全表示，那么可以吧$a_{T}$带回到优化目标的最后一项中，然后，最后一项可以写成：

\[V(s_T)=\frac{1}{2}s_T^TV_Ts_T+s_T^Tv_T\\ V_T=C_{s_T,s_T}+C_{s_T,a_T}K_T+K^T_TC_{a_T,s_T}+K^T_TC_{a_T,a_T}K_T\\ v_T=c_{s_T} + C_{s_T,a_T}k_T+K^T_TC_{a_T}+K^T_TC_{a_T,a_T}k_T\]

同理，可以类似得到上一时刻的动作$a_{T-1}$的表示。总的来说，LQR会倒叙执行下面的伪代码（代码里的x就是s，u就是a）

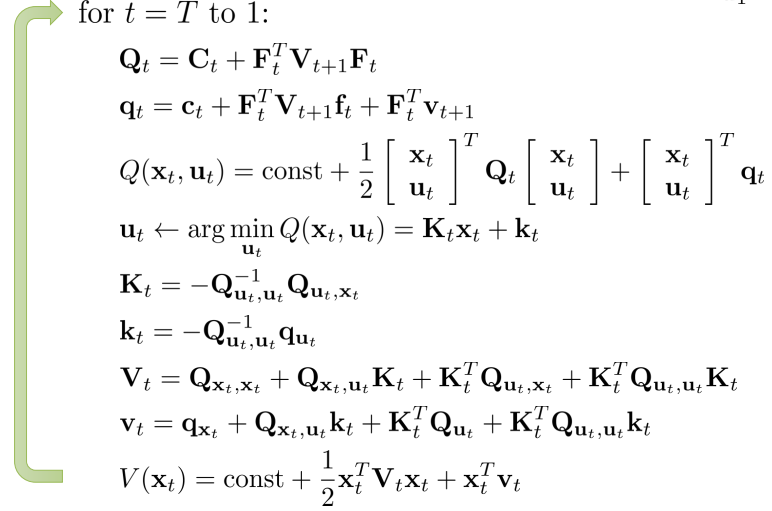
当执行到t=1的时候，就用已知的$s_{1}$来正推回来，得到完整的action序列

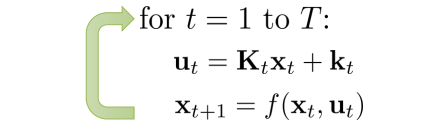
9.3.2 Non-linear dynamics case

LQR是假设了dynamics是线性的情况，实际上dynamics很可能是非线性的。这就要用到iterative LQR 算法了，他是吧非线性的问题用local linear的方式来近似。近似的方式就是用泰勒展开。对dynamics用泰勒一阶展开成线性的，对cost用二阶展开成quatratic的

\[f(s_t,a_t)\approx f(\widehat{s}_t, \widehat{a}_t)+\triangledown_{s_t,a_t}f(\widehat{s}_t, \widehat{a}_t)\begin{bmatrix} s_t-\widehat{s}_t \\ a_t-\widehat{a}_t \end{bmatrix}\\ c(s_t,a_t)\approx c(\widehat{s}_t, \widehat{a}_t)+\triangledown_{s_t,a_t}c(\widehat{s}_t, \widehat{a}_t)\begin{bmatrix} s_t-\widehat{s}_t \\ a_t-\widehat{a}_t \end{bmatrix} + \frac{1}{2}\begin{bmatrix} s_t-\widehat{s}_t \\ a_t-\widehat{a}_t \end{bmatrix}^T\triangledown_{s_t,a_t}^2c(\widehat{s}_t, \widehat{a}_t) \begin{bmatrix} s_t-\widehat{s}_t \\ a_t-\widehat{a}_t \end{bmatrix}\]

这个问题就转化成了在linear dynamics了，只不过state和action都变成了新的表示：$s_{t}-\widehat{s}{t}$，$a{t}-\widehat{a}_{t}$。下面是他的伪代码