Why Sampling

在大多机器学习的任务中，我们对模型参数$\theta$的求解对象都是它的后验分布$P(\theta \mid X) \propto P(X\mid \theta )P(\theta)$。如果我们幸运的知道，先验和似然是共轭的关系，后验就和先验服从同一类分布形式，那么我们可以简化计算，进一步得到参数后验的表达式$P(\theta \mid X)$。实际上往往是不共轭的，虽然我们知道参数的先验$P(\theta)$和似然$P(X\mid \theta )$的表达式，但是后验$P(\theta \mid X) \propto P(X\mid \theta )P(\theta)$往往是一种形式很复杂的分布，难以求出参数的均值方差等统计特性。所以我们需要Sampling，从某个分布中来抽样，得到一些样本，然后根据这些样本，我们就可以得到对该分布特性的估计。比如，Sampling可以用做对概率图模型上的(基于粒子的)近似推断

关于采样方法，个人不成熟的分为下面两种：

两次采样数据之间相互独立

比如：CDF Sampling, Reject Sampling, Adaptive Rejection Sampling, Importance Sampling
两次采样数据之间不独立

比如：MCMC, Slice Sampling

1. 独立数据采样

1.1 CDF Sampling

累积分布函数（Cumulative Distribution Function，CDF）是一个随机变量X的概率分布相对应的不减函数，是概率密度函数的积分，记为$F(x)=P(X \le x)$。CDF sampling最简单的抽样方法，该方法需要已知CDF的逆函数。具体的算法步骤是

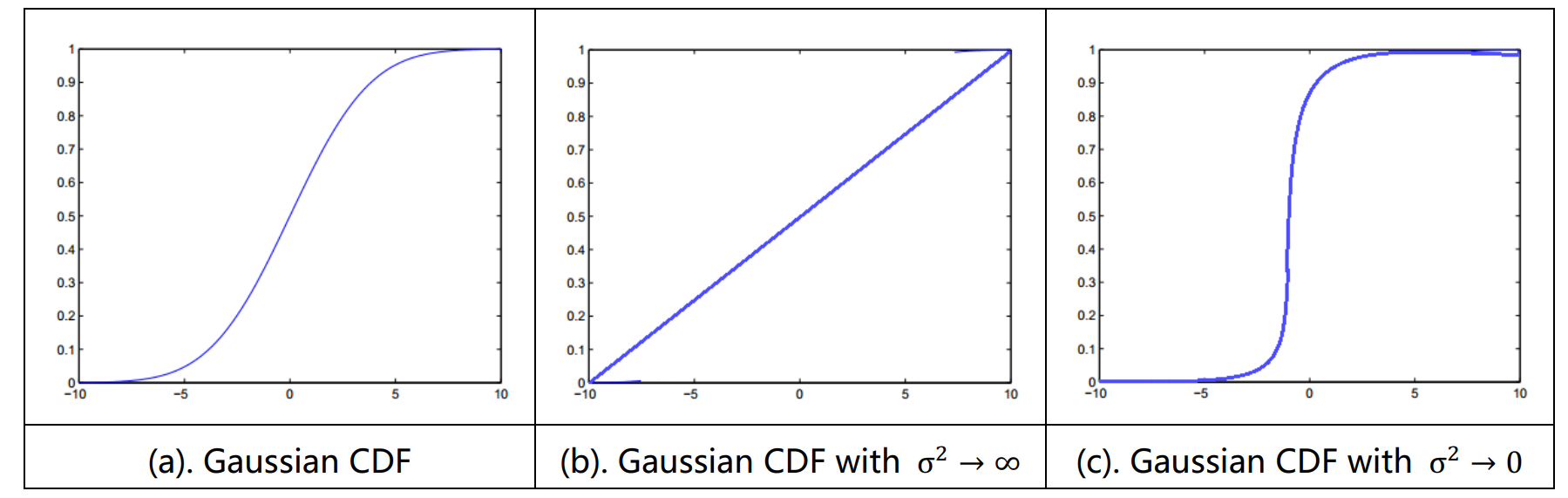
以一维高斯分布为例，其高斯的CDF如下图所示。CDF Sampling首先对$[0,1]$上进行均匀分布采样，将采样值$Y_{0}$带入高斯CDF的逆函数中，求得一个采样值$X_{0}$（即对图中的Y轴进行采样，求得对应的X值）。如下图所示，图(b)中可以看出，当方差很大的时候，高斯分布变得很平坦，每个x被采样到的几率等大; (c)当方差很小的时候，高斯分布绝大部分质量都集中在均值附近，使得采样点也集中与均值处。很明显CDF采样的缺点就是其逆函数的计算十分困难

1.2 Rejection Sampling

由于待采样分布P(X)的复杂性，拒绝采样旨在利用一个简单的分布$Q(X)$，并构造接受域和拒绝域，然后对简单分布$Q(X)$进行采样（这样的Q分布叫做Proposal Distribution），并且将落在接受域中的采样数据视为对原始分布$P(X)$的采样数据。当然这样的$Q(X)$需要满足一定的条件：要求$Q(X)$在任何处的值都要大于$P(X)$，由此一来才可以定义接受域（$P(X)$下的面积）和拒绝域（$Q(X)$以下，$P(X)$以上的面积）。然而，这个条件显然是不可能的成立的，由于两者的积分面积都等于1，所以不可能$Q(X)$在任何处的值都要大于$P(X)$。因此为了保证这个条件，通常会利用一个比较大的数$M$与$Q(X)$相乘，对Q(X)进行放大处理，如下图所示：

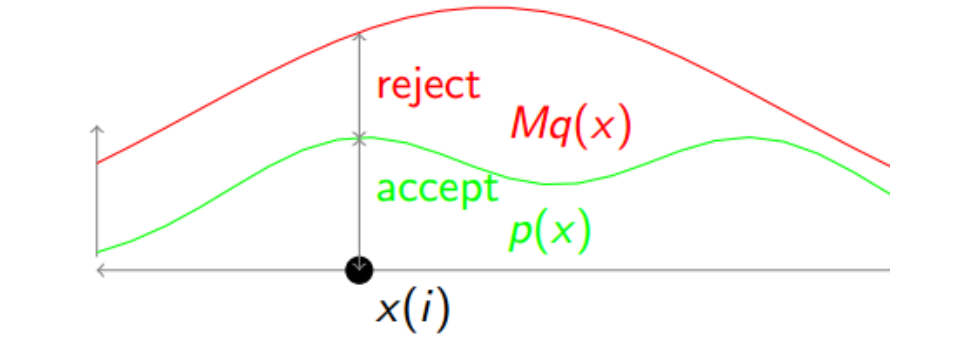
所以拒绝采样的步骤是：

具体来说，先根据$Q(X)$进行采样一个$X_{i}$，然后再从$Q(X_{i})$到X坐标轴的这条竖线上进行均匀采样，如果采样点a落在reject区域就不要这个值，落在accept区域就接受$X_{i}$。明显当两个分布$Q(X)$和$P(X)$比较接近的时候，采样值被拒绝的几率小，相反如果两者差距大，则拒绝的几率就大。所以还是比较合理的。问题是M的放大倍数和$Q(X)$的选择不好确定，导致可能大多数都被reject了，所以采样的效率不好，大多会原地踏步，由此有了Adaptive Rejection Sampling。

1.3 Adaptive Rejection Sampling

该方法旨在解决$Q(X)$的选取问题，加快Rejection Sampling的抽样速度。它通过$P(X)$来直接构造$Q(X)$，比如，如果$P(X)$是log-concave的（$logP(X)$是concave的，比如高斯不是concave的，但是$log(高斯)$是concave的），我们可以通过在$logP(X)$上进行找点做切线来构造一个由多个线性函数组成的分段函数$Q(X)$，如下图所示

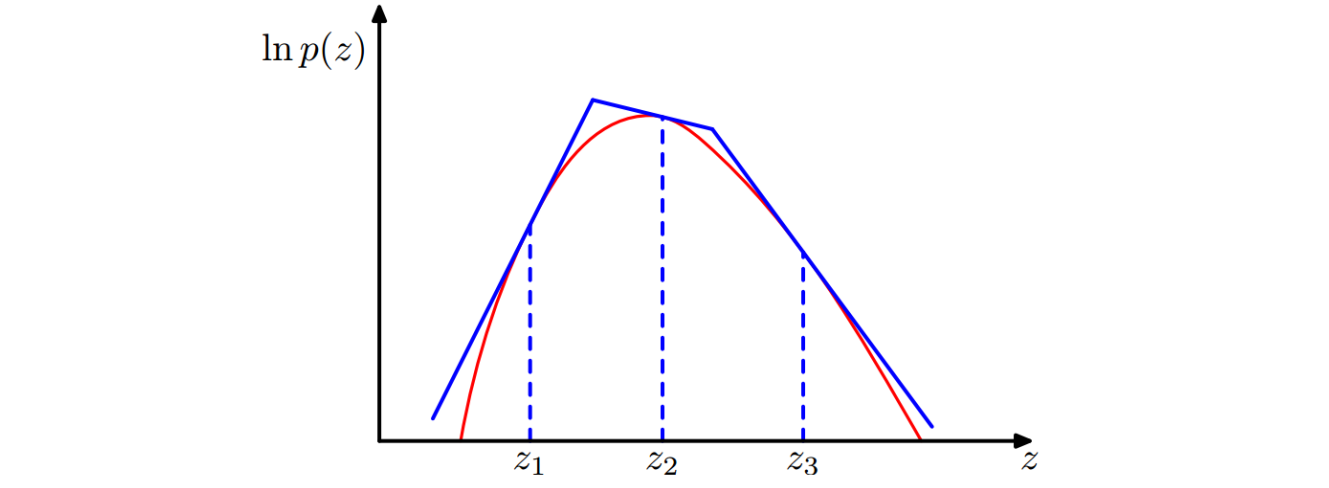
但是以上的采样方法，都将面临一个维度问题，在高维度的情况下，这种采样方式是特别困难的。以PRML中的例子来说明，考虑$P(X)$服从零均值，协方差为$\sigma^2 I$的D维高斯分布, 其中$I$是单位矩阵。根据拒绝采样方法，很自然的选择$Q(X)$也是1个零均值的高斯分布，协方差为$\sigma_{q}^2 I$, 很明显，为了得$MQ(X)\ge P(X)$的M值存在，我们必须有$\sigma_{q}^2 I \ge \sigma^2 I$。在D维的情形中， $M$的值为$(\frac{\sigma_{q}^2}{\sigma^2} )^D$，因此接受率随着维度的增大而指数地减小

1.4 Importance Sampling

重要性采样提供了直接近似期望的框架方法，它假定直接从$P(X)$中采样方法完成，但是对于任意给定的$X$值，我们可以很容易地计算$P(X)$。如此为了计算其期望$E(f(X))=\int f(X) P(X) dX$，我们希望对$P(X)$值大（质量大）的区域中尽可能多的进行采样，因为这部分的样本对期望的计算发挥的作用更大。重要性采样，把容易被采样的新的分布$Q(X)$作为目标采样分布，并且赋予这些采样的样本一定的权重，整个样本上的不同大小的权重值的则构成了真实的$P(X)$的采样数据，如下所示

\[E(f(X))=\int f(X) P(X) dX \mbox{ //这里的}X_i \sim P(X) \\ =\int f(X) \frac{P(X)}{Q(X)}Q(X) dX \mbox{ //这里的}X_i \sim Q(X) \\ =\int f_{new}(X) P(X) dX \\ \approx \frac{1}{N}\sum_{i=1}^N f(X_i) \frac{P(X_i)}{Q(X_i)} = \frac{1}{N}\sum_{i=1}^N f(X_i) P_{new}(X_i)\]

其中$Wi=\frac{P(X_{i})}{Q(X_{i})}$ 称为重要性权重（importance weights），从而，我们能从简单的分布$Q(X)$中进行采样，通过对于样本权重的控制，还原目标分布$P(X)$的信息。需要指出，重要性采样IS和拒绝采样RS是有区别和联系的：

RS 每个数据的权重是相同的，通过拒绝部分样本（概率低的样本）来force采样数据服从$P(X)$
IS 每个数据的权重是不同的，是通过weight的大小来刻画分布，所以的样本都被保留下来
两者，两次采样样本之间是没有任何关系的，是独立的进行每次的采样。同时，两者如何选取$Q(X)$是至关重要的，对于IS来说，如果$Q(X)$与$P(X)$之间的相交面积很小很小，如下

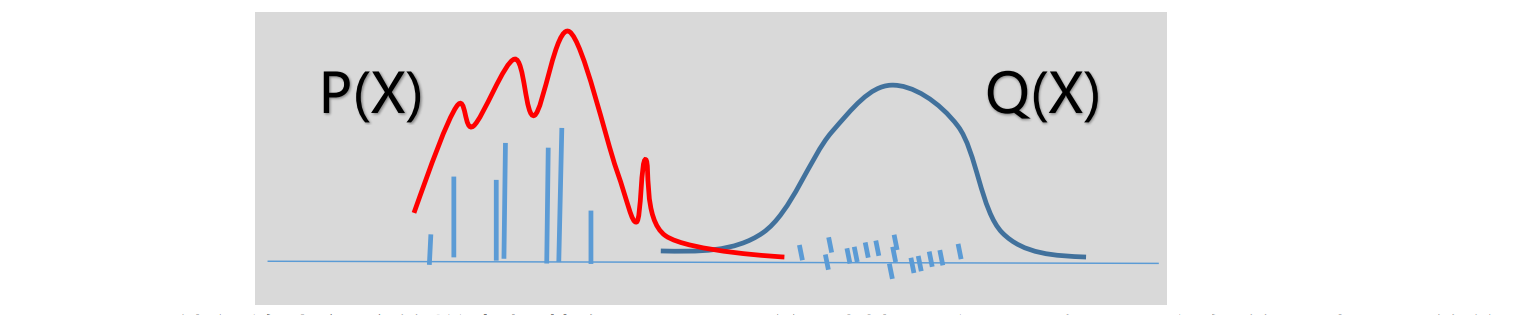
使得绝大部分的样本都落在$Q(X)$下，并且其权重很小，如果要很好的反映$P(X)$的信息，需要进行多次的IS采样（因为小概率落在$P(X)$下的权重很大）,其效率决定于PQ的相似度。当然，为了避免这种情况，往往倾向于选择具有长尾特定的Q分布，也可以使用Weighted Resampling(或者叫Sampling-Importance-Sampling)，这个方法在后文会介绍。下面再介绍几个重要性采样的变种

1.4.1 Normalization Importance Sampling

从上面我们已经看出，普通IS的假设是：已知$X=x$，我们可以容易的计算出$P(X=x)$，但是在实际情况下，这有可能是不成立的，比如在有向图模型中计算$P(X\mid e)=P(X,e) / P(e)$，其中e代表evidence；再比如MRF中计算$P(X)=P’(X) / Z$，其中Z是partition function。因此我们引入Normalized Importance Sampling，用来应对这种情况：我们不能直接计算出$P(X)$，只能得到$P’(X)=\alpha P(X)$。此时，我们有

\[E(f(X))=\int f(X) P(X) dX \mbox{ //这里的}X_i \sim P(X) \\ =\int f(X) \frac{P(X)}{Q(X)}Q(X) dX = \frac{1}{\alpha} \int f(X) \frac{P'(X)}{Q(X)}Q(X) dX\]

令 $r(X)=\frac{P’(X)}{Q(X)}$,有下式成立：

\[\int r(X)Q(X)dX = \int \frac{P'(X)}{Q(X)} Q(X) dX = \int \alpha P(X) dX = \alpha\]

所以有：

\[E(f(X))=\frac{1}{\alpha} \int f(X) \frac{P'(X)}{Q(X)}Q(X)dX\\ =\frac{\int f(X)r(X)Q(X)dX}{\int r(X)Q(X)dX} \approx \frac{\sum_{i=1}^m f(X_i)r(X_i)}{\sum_{k=1}^mr(X_k)} \mbox{ //X采样自Q}\\ =\sum_{i=1}^m f(X_i) \frac{r(X_i)}{\sum_{k=1}^m r(X_k)}\]

Normalized版本和un-normalized的区别是：

un-normalized importance sampling的估计量是无偏的（$E_{Q}(f_{new}(X))=E_{P}(f(X))$），另一个不是
normalized importance sampling的方差，在实际使用中会更小。

1.4.2 Likelihood Weighting Sampling

这种采样算法是Normalized IS在有向图模型上的一个特例。如下左图，我们令Χ为网络中的所有节点，以$E \subset Χ$表示已观察到的变量集合。为了对$(x_{1},x_{2}, …, x_{[X]} )^M$ 进行采样（其中，$[X]$表示数据维度，$M$表示采样数据的个数），对于$E$中的变量$X_{i} \in E$，他的采样值就等于他的观察取值，$X_{i}=x_{i}$，对于不在$E$中的变量，我们对$P(X_{i} \mid Pa(X_{i}))$进行采样，其中$Pa(X_{i})$表示$X_{i}$的父节点。其步骤如下所示

举个栗子，现已知$E={G=g^2,I=i^1}$，我们可以计算出$P(D,S,L,G=g^2,I=i^1 )$，但是出于某些神秘的原因我们不能直接得到$P(G=g^2,I=i^1 )$，我们还想求的$P(D,S,L\mid G=g^2, I=i^1)$。那么现在，我们采用Normalized Importance Sampling进行采样，首先$Q$的选择是个大问题，但是我们已知了$E={G=g^2,I=i^1 }$，去掉指向节点$G$, $I$的边，可以得到右图，其表达出的分布就是我们所需的$Q$，

\[Q(D,S,L)=P(D)P(S\mid I=i^1) P(L \mid G=g^2)\]

这样得到的$Q$将产生更多的独立性关系，简化$Q$联合概率表示，去除其父节点的连边，相当于改变$E$中的节点的概率取值，即已知$G=g^2,I=i^1$，则$P(G=g^2 )=P(I=i^1 )=1$ （但是这不是说，原始的概率取值也跟着改变，这里只是给一个图形化的解释而已）。那么现在对$Q$进行采样，就只用分别的采样三部分

\[d \sim P(D) \\ s \sim P(S \mid I=i^1) \\ I \sim P(L \mid G=g^2)\]

在得到采样点之后，还需确定点的权重。此时，权重仅仅由E中的节点在给定它的父节点下的概率的乘积确定：

\[r(X)=\frac{P'(X)}{Q(X)}=\frac{P(D,S,L,G=g^2,I=i^1)}{P(D)P(S \mid I=i^1)P(L \mid G=g^2)} \\ =\frac{P(D)P(I=i^1)P(G=g^2 \mid D, I) P(S \mid I=i^1) P(L \mid G=g^2)}{P(D)P(S \mid I=i^1)P(L \mid G=g^2)} \\ =P(I=i^1) P(G=g^2 \mid D, I)\]

值得注意的是，likelihood weighting算法是先带权采样，最后才进行权重的归一化操作。说起来还是太抽象，下面我们做几轮采样的实际例子：

初始化权重$w = 1$，$E={G=g^2,I=i^1}$

采样$D$，$D$不在$E$中，进行采样，若得到$D=D^0$；
采样$I$，$I$在E中，直接取值$I=i^1$，更新权值$w = wP(I=i^1)=1.00.3=0.3$；
采样$G$，G在E中，直接取值$G=g^2$，更新权重$w = wP(G=g^2 )=0.30.08=0.024$
采样$L$，若$L=l^1$
采样$S$，若$S=S^0$ ，然后我们得到下面的表格

初始化权重$w = 1$，$E={D=D^1,I=i^0}$

采样$D$，$D$在$E$中，直接取值$D=D^1$，更新权重$w = w*P(D=D^1 )=0.4$
采样$I$，$I$在$E$中，直接取值$I=i^0$，更新权值$w = wP(I=i^0 )=0.40.7=0.28$；
采样$G$，若$G=g^0$
采样$L$，若$L=l^1$
采样$S$，若$S=S^0$，然后我们得到下面的表格

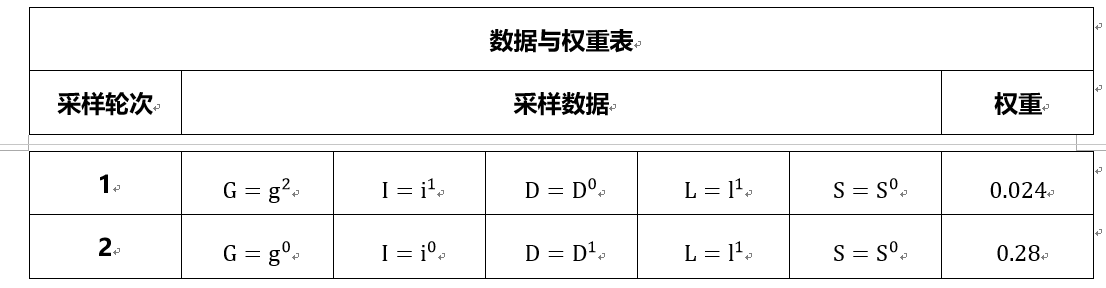
就这样依次的不断采样，得到最后的样本集合。好了，由于我们比较懒，现有的样本就只有上面两个，那么我们就可以求概率啦，比如边缘概率

\[P(D=D^1) = \frac{0.28}{0.28+0.024} = 0.92105\]

恩恩，跟图中的真实值差很远，毕竟我们只有两个样本嘛。最后总结一下，可以发现，如果E中的节点全是根节点，那么所有样本的权重都会是一样的；另一方面，如果E中的节点都是叶子节点，如果观测值发生的几率小，那么样本的权值也很有可能会很小（因为此时，权值只与观测节点有关，也就是E中的节点有关，并且他们在Q中没有父节点，使得他们可以看做是先验。）

1.4.3 Weighted Resampling (Sampling-Importance Sampling)

1.4.4 Sequential Importance Sampling

因为Importance Sampling在高维度上表现不好，比如如果$P(X)$是一维零均值高斯，并且要求采样值$x$必须大于０，那么采出来一半的数据都不能用，如果$x$的维度增加的话，比如20维，那么平均采集$2^20$次才有一个样本有效。为了解决这个问题，引入Sequential Importance Sampling(或者Particle Filtering，动态系统中的一种)，旨在对每个样本一维一维的进行采样，在这个过程中$Q$分布也跟着慢慢的变化。既然它又叫做Particle Filtering，那么先说说什么是Filtering操作：给定$T = 1$到$t$时间的观测值，我们希望对时间$T=t$时的状态进行求解，目标为$P(X_{t} \mid Y_{1},Y_{2},…,Y_{t})$。下面，给定图模型，对filtering的求解进行推导。

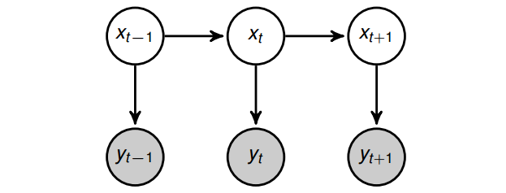
\[P(X_t \mid Y_1, Y_2, ... , Y_t) = \frac{P(X_t, Y_1, Y_2, ... , Y_t)}{P( Y_1, Y_2, ... , Y_t)} \propto P(X_t, Y_1, Y_2, ... , Y_t)\]

根据有向图上的独立性关系（给定$X_{t}，Y_{t}$与其他节点条件独立），对上式进行化解

\[P(X_t \mid Y_1, Y_2, ... , Y_t) \propto P(X_t, Y_1, Y_2, ... , Y_t) =P(Y_t \mid X_t) P(X_t \mid Y_1, Y_2, ..., Y_{t-1})\]

其中，$P(Y_{t} \mid X_{t})$在HMM或者动态系统中称为Measurement Probability，而另一项$P(X_{t} \mid Y_{1},Y_{2},…,Y_{(t-1)})$表示，给定一组观察，对下一个时刻状态的Prediction。现在我们回到正题，假设现在我们选好了$Q$分布，我们希望从中开始采样，由于$X$的维数太高，我们首先对第一维进行采样（注$X_{(1:M)}$中的$1:M$表示第一维到第M维）。已知目标为$X_{1}$，通过把$X$的第$2:M$维积分积掉就可以得到，即下式，此时的权值为$r(X_{1})$

\[P(X_1) = \int P(X_{(1:M)}) dX_{(2:M)} \\ r(X_1) = \frac{P(X_1)}{Q(X_1)} \mbox{ }\mbox{ }\mbox{ }\mbox{ } X_1 \sim Q\]

在获取了$X_{1}$之后，考虑$X_{2}$，也通过积分的形式得到$X_{(1:2)}$，那么只用根据$Q(X_{2} \mid X_{1})$对$X_2$采样我们就可以获得$X_{(1:2)}$

\[P(X_{1:2}) = \int P(X_{(1:M)}) dX_{(3:M)} \\ r(X_{1:2}) = \frac{P(X_{1:2})}{Q(X_{1:2})} =\frac{P(X_{1:2})}{Q(X_1)Q(X_2 \mid Q_1)} \mbox{ }\mbox{ }\mbox{ }\mbox{ } X_{1:2} \sim Q\]

这个过程中，在采x的第二维的时候，只用从Q的条件概率里进行采样就行了，以此类推。并且，我们还可以用上一次的信息来sequencial的更新权重

\[r(X_{1:t-1})=\frac{P(X_{1:t-1})}{Q(X_{1:t-1})} \rightarrow Q(X_{1:t-1}) = \frac{P(X_{1:t-1})}{r(X_{1:t-1})} \\ r(X_{1:t}) = \frac{P(X_{1:t})}{Q(X_{1:t-1})Q(X_{t}\mid X_{1:t-1})} = r(X_{1:t-1}) \frac{P(X_{1:t})}{Q(X_t\mid X_{1:t-1})P(X_{1:t-1})}\]

2. 不独立数据采样

（这类别是我瞎编的）不独立数据采样顾名思义就是前后两次采样点之间是不独立获取的，其实前文说到的Sequential Importance Sampling也应该算是不独立采样的类型，两次采样点之间通过权值相依赖，采样数据通过条件概率获取，我还是把它作为IS的扩展放在上面了。

2.1 Monte-Carlo (MCMC)

不同于以上的采样方式，MC方法虽然也会动态的构造一个proposal distribution $Q$，但是所采样的数据仍然是来自于原始分布P，而不是Q

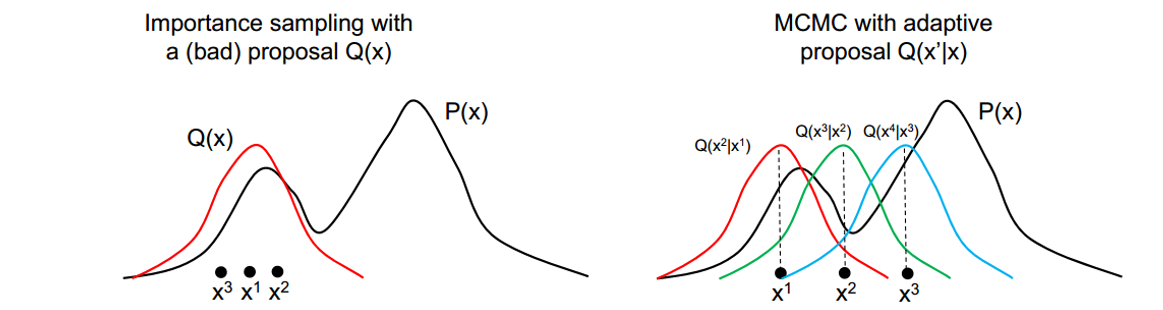
在图模型上的采样几乎都是用MC方法，因为MC直接对P分布进行采样，当P分布很难算的时候，正好可以做inference来解决，所以MC和图模型简直是天生一对？但是虽然MC方法可以应对高维问题，但是在高维情况下的一些小概率事件很难被采样到，而且，对于像MRF一样的分布（自带一个partition function Z）是不适用的，除非我们知道了这个Z。下面简要说明所有的MC方法的理论基础，具体分析就不说明了

通过使用马氏链的收敛与平稳分布，在给定的概率分布$P(X)$下，我们如果能构造一个转移矩阵为$P$的马氏链，使得该马氏链的平稳分布正好是分布$P(X)$，那么我们从任意一个初始状态，沿着这条马氏链转移，得到一个转移序列$X_{0},X_{1},…,X_{n},X_{(n+1)},…$ ，如果马氏链在第$n$步收敛，那么目标$P$的采样就是$X_{(n+1)},X_{(n+2)},…$，而$n$之前的采样叫做burn in，这就是MCMC采样的重要思想！但是这里很重要的一个问题就是，$n$值得确定，这一般都是人为，凭经验的。那如何去构造这样的转移矩阵$P$使得平稳分布就是我的目标分布呢？我们是用细致平稳条件来构造

其中，$P_{ij}$表示从状态$i$转移到状态$j$，$\pi (i)$表示处于$i$状态的概率。这个定理表示，状态$i$与状态$j$之间的相互转移是能量守恒的，所以是平稳的，具体的数学证明就从略咯。下面具体介绍两种MCMC采样的算法，MH和Gibbs采样。

2.2 MH Sampling

现已知目标分布为$P(X)$，我们构造转移矩阵$Q(X)$，让他满足细致平稳条件:

\[P(X_i)Q(X_j \mid X_i) = P(X_j) Q(X_i \mid X_j)\]

当然现实又是残酷的，这样的$Q(X)$还是很难构造的，所以我们需要一个更松弛的条件，接受率$\sigma$，我们希望满足

\[P(X_i)Q(X_j \mid X_i)\sigma(X_j \mid X_i) = P(X_j) Q(X_i \mid X_j)\sigma (X_i \mid X_j) \\ \mbox{其中:} \left\{\begin{matrix} \sigma(X_i \mid X_j) = P(X_i) Q(X_j\mid X_i) \\ \sigma(X_j \mid X_i) = P(X_j) Q(X_i\mid X_j) \end{matrix}\right.\]

这样就恒等啦。也就是说，如果令$Q’(X_{j}\mid X_{i})=Q(X_{j}\mid X_{i})\sigma (X_{j}\mid X_{i})$，从此马氏链$Q’$的平稳分布就是目标$P(X)$了，当状态$i$以概率$Q(X_{j}\mid X_{i} )$转移到状态j时，我们以$\sigma(X_{j} \mid X_{i})$的接受率接受这个跳转。所以按照这个思路，算法执行过程为

但是这样的问题是，接受率$\sigma$，可能会比较小，从而导致大部分的样本都被拒绝，使得采样进展和收敛的进度都很慢很慢，比如

\[P(X_i)Q(X_j \mid X_i)*0.1 = P(X_j) Q(X_i \mid X_j)*0.2\]

改进的方法很直观，我们直接对等式做放大处理，使得两者中最大的那个数，放大到1，比如这里可以同时乘以5，那么得到

\[P(X_i)Q(X_j \mid X_i)*0.5 = P(X_j) Q(X_i \mid X_j)*1.0\]

那么要从状态$i$到状态$j$，需要接受率至少为$\sigma=min{\frac{P(X_{j} )Q(X_{i}\mid X_{j} )}{P(X_{i})Q(X_{j}\mid X_{i})}, 1}=0.5$，需要注意的是，这样做我们并没有破坏平稳条件:

\[P(X_i)Q(X_j \mid X_i)\sigma(X_j \mid X_i) =P(X_i)Q(X_j \mid X_i)min\{\frac{P(X_{j} )Q(X_{i}\mid X_{j} )}{P(X_{i})Q(X_{j}\mid X_{i})}, 1\}\\ =min\{ P(X_j)Q(X_I \mid X_j), P(X_i)Q(X_j\mid X_i) \}\\ =P(X_j) Q(X_i \mid X_j) min\{1, \frac{P(X_{i} )Q(X_{j}\mid X_{i} )}{P(X_{j})Q(X_{i}\mid X_{j})} \} \\ = P(X_j) Q(X_i \mid X_j)\sigma (X_i \mid X_j)\]

到这里，MH算法终于浮出了水面，如下所示

下面我们来看一个MH采样的例子

接下来，说说MH的缺点：其实从例子里可以看出，如果proposal distribution $Q(X)$和$P(X)$的关联性很差的话，会很影响采样的收敛速度，比如讲例子中的$Q$的方差减小，虽然接受率会提高，但是遍历整个空间的将变得很慢，另一方面，若增大$Q$的方差，那么样本被拒绝的概率明显会增加。其中，Hybrid Metropolis Hasting是一种解决办法，他的一个关键思想是考虑了采样的方向与步长，该算法对P(X)的对数求导

\[\frac{\partial log P(X) }{\partial X} = \frac{P'(X)}{P(X)}\]

其中，$P(x)$控制采样步长，$P’(x)$控制方向，导数的方向总是向着$P(x)$上升的方向，所以是向着分布的峰值处采样，并且此时对应的采样的步长$1/P(x)$ 小，此处的采样样本数目很多。

2.3 Gibbs Sampling

Gibbs采样是对MH算法中接受率的改进，因为毕竟MH的接受率不是1，Gibbs采样旨在找一个转移矩阵，每次的使得接受率恒为1，所以Gibbs采样可以看做是MH算法的一个具体情况。总的来说，Gibbs采样是基于坐标轴的采样方法。我们考虑二维的例子。给定一个概率分布$P(X,Y)$，考虑横坐标相同的两个点$A(X_{1},Y_{1})$, $B(X_{1},Y_{2})$。

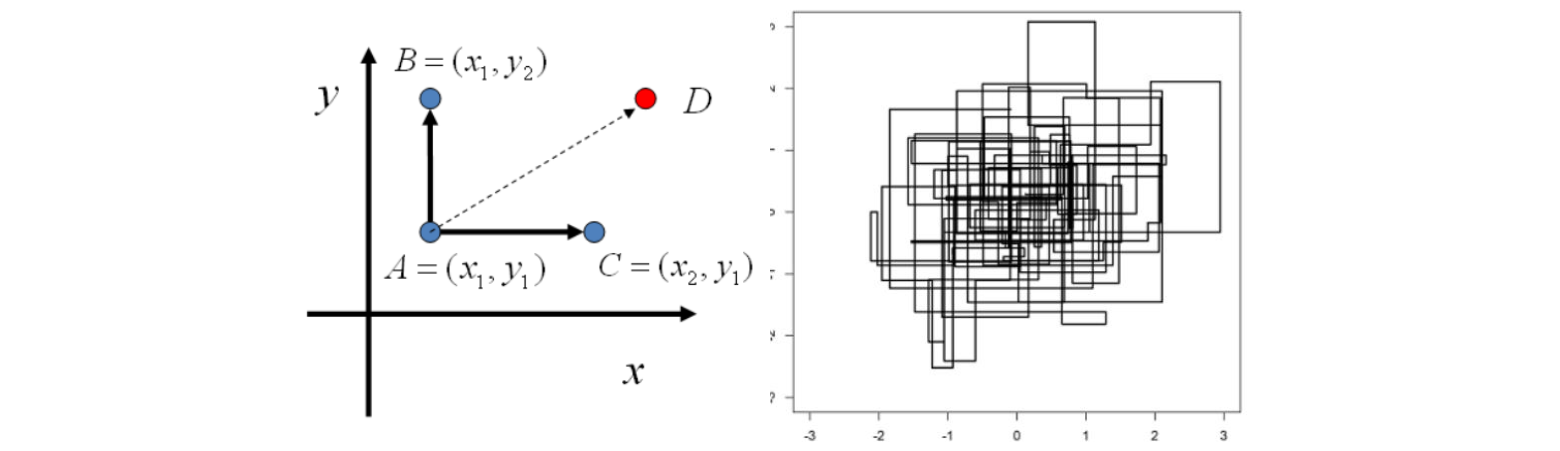
\[\left\{\begin{matrix} P(X_1,Y_1)=P(X_1)P(Y_1 \mid X_1) \\ P(X_1,Y_2)=P(X_1)P(Y_2 \mid X_1) \end{matrix}\right.\]

那么有

\[P(X_1, Y_1) P(Y_2 \mid X_1) = P(X_1, Y_2)P(Y_1 \mid X_1)\]

这个式子说明，沿着坐标轴方向上，任意两点之间的转移都满足细致平稳条件。所以在二维或者高维情况下的Gibbs采样算法很简单，如下所示，当然对于Gibbs采样也是有burn in阶段的

从算法中可以看到，采样信息是立即就使用的，在$X_{1}^{t+1}$ 会在对$X_{2}^{t+1}$采用时被使用到。下面举一个例子进行说明。给定下图的贝叶斯网络，节点都是二值得（T, F），我们要对其变量进行Gibbs采样，假定在t=0时刻，所有变量取值为F，并且我们的采样顺序固定为B, E, A, J, M

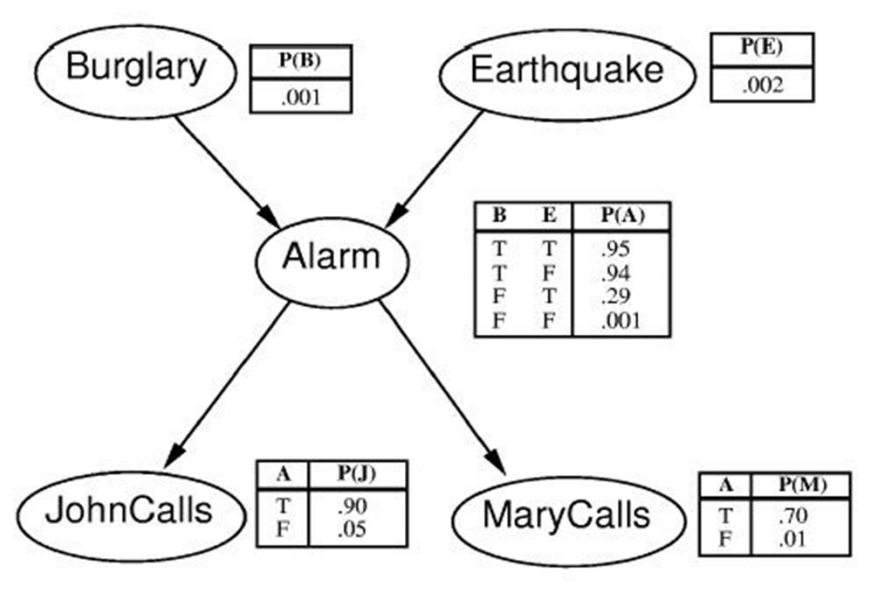
现在给定其他变量，我们对B进行采样，对上图B在给定A的条件下，与E节点是相互依赖的，所以存在

\[P(B \mid E,A,J,M)=P(B \mid A,E) = \frac{P(B,A,E)}{P(A,E)} = \frac{P(B)P(E)P(A \mid E, B)}{P(A,E)} \propto P(B) P(A \mid E, B)\\ P(B=F \mid A=F, E=F) \propto P(B=F) P(A=F \mid E=F, B=F) = 0.999 * 0.999 \\ > P(B=T \mid A=F, E=F)=0.001 * 0.06\]

假设根据上式，我们以概率采样得B=F，我们便可以更新下表

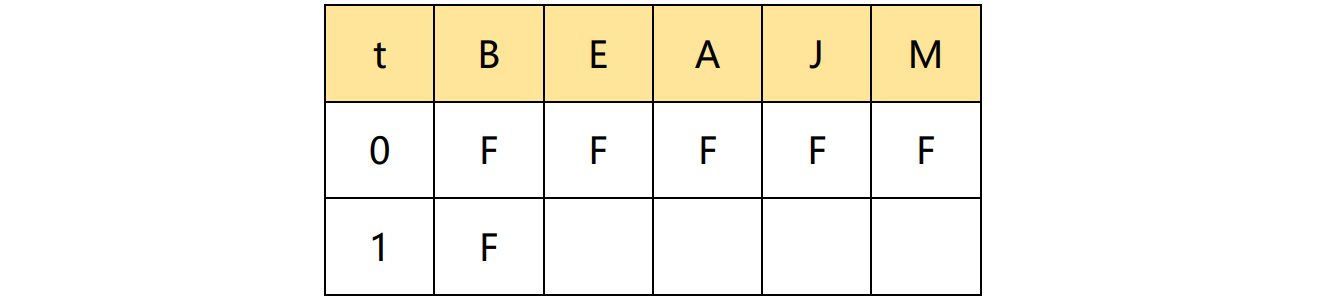
同理，我们采样 E 节点

\[P(E \mid B,A,J,M)=P(E\mid A,B) \propto P(E)P(A\mid E,B) \\ P(E=F \mid A=F,B=F)=0.998 * 0.999\]

假设，虽然E=F的概率很大，但是我们的采样值是F=T，然后更新表格

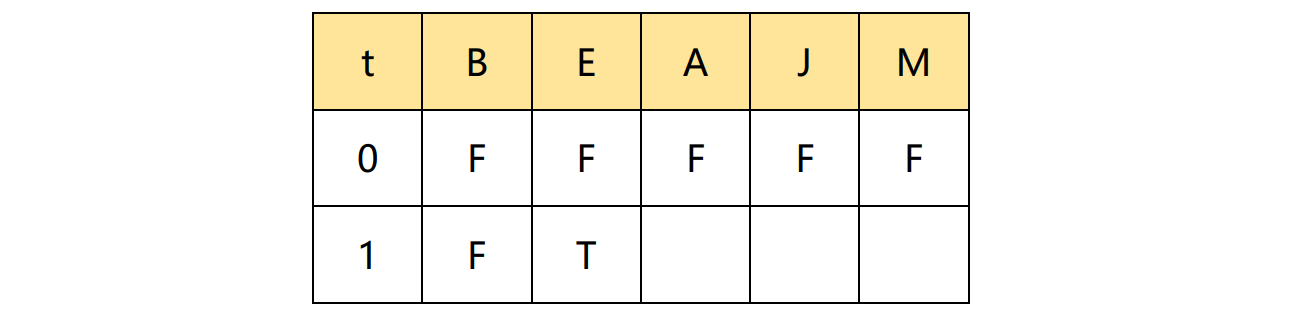
最终这么一直采样下去，就可得到最后的采样样本

2.4 Slice Sampling

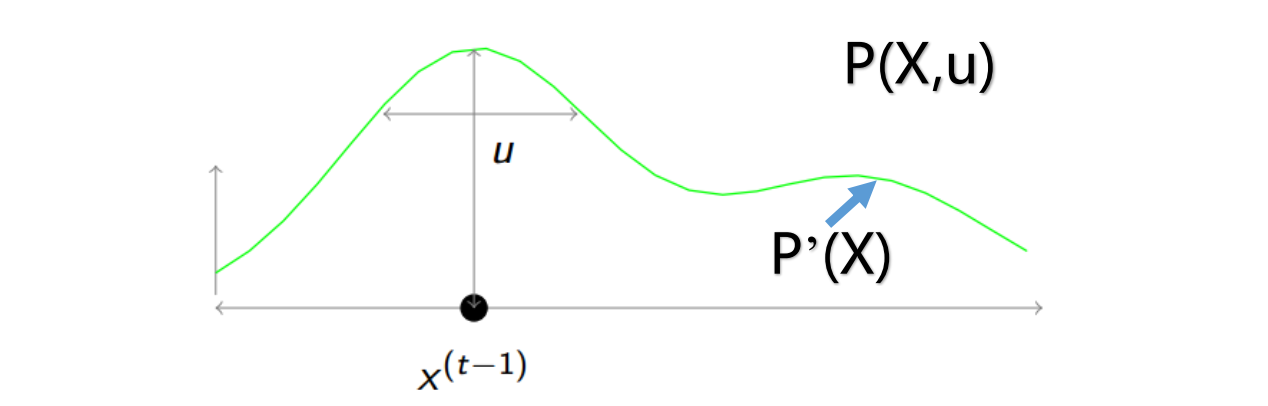
之前有一点点的提到，对于MH（包括Gibbs）的缺点就在于采样步长的敏感性，其步长是由转移条件概率的方差确定的，如果方差太小，接受率高，但是收敛执行很慢；方差大，则拒绝率高。Slice Sampling则旨在自适应的调节步长来匹配分布特性，它的假定和NIS一致，认为不能直接计算出$P(X)$，只能得到一个非归一化的分布$P’(X)=\alpha P(X)$。该算法涉及到引入一个新变量$u$，然后从联合分布$P(X,u)$中进行采样。其联合分布构造如下

\[P(X,u)=\left\{\begin{matrix} \frac{1}{Z} \mbox{ if } 0 \leq u\leq P'(X) \\ 0 \mbox{ otherwise} \end{matrix}\right.\]

其中，$Z=\int P’(X) dX=\alpha$，也就是说$P(X)=P’(X)/Z$。这样的联合概率分布满足两个性质，第一，在区间$ 0\leq u\leq P’(X)$中，$P(X,u)$是均匀分布的（因为Z是常数）；第二，如下式

\[\int P(X,u) du=\int_0^{P'(X)} \frac{1}{Z} du = \frac{P'(X)}{Z} = P(X)\]

所以，Slice Sampling想法就是对联合概率$P(X,u)$进行采样之后，消去$u$之后就是我们目标$P(X)$的采样值。当然，Slice采样并不是这个步骤，而是如下所示：先给定$X^{t-1}$的值，对$P(X,u)$在面积$0\leq u\leq P’(X)$上进行均匀采样$u$，然后再$P’ (X)>u$的区域（就是过点采样点$u$，做垂直于$U$轴的线，把$P’(X)$给切片）的切片上进行均匀采样，得到下一个样本$X^t$。所以Slice Sampling更容易在波峰处进行采样

在上图的例子中，一切都显得这么顺利，当然实际上并不是这样，因为我们对$P’(X)$进行切片的时候，很可能不切到一个波峰，此时对多个波峰进行均匀采样是不适合的，因为他们取值并不连续，如下图所示，存在了两个波峰的切片

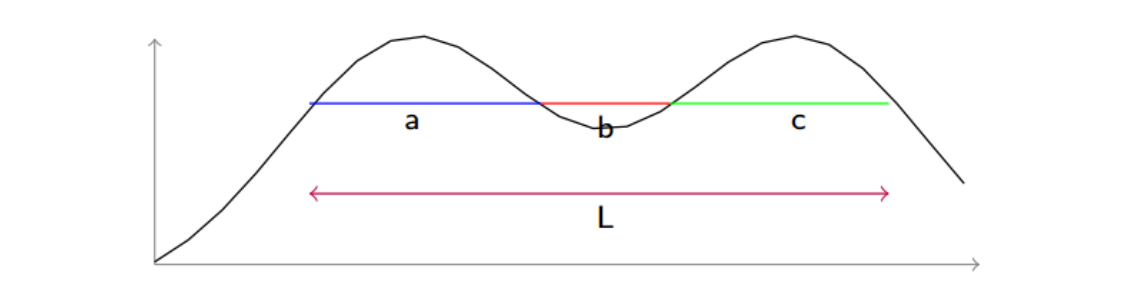
解决这个计算问题引入Shrink algorithm，该算法在各个波峰，通过凹进去的部分，联接起来，组成一个大切片（也就是图中，通过$b$，连接了$ac$，然后$abc$看做一个切片，区间是$[a_start,c_end]$）进行均匀采样。假设$X^{t-1}$在a下方，采样值$X^{t}$位于了$b$上，假设是$b1$，则我们需要做收缩处理，把采样区间变成$[a_start,b1]$，如果落在非b区域，则接受，否则再做一个收缩。

这么做的话，两次最终的采样值更有可能在同一个比较近的距离，意思是如果前一次的采样值落在$a$中，那么下一次的采样值落于$a$中的可能性比落入$c$中的可能性更大，因为如果落在了$b$中，还是可以缩回来到$a$中的。但是需要保证，上一次落在$a$的概率和下一次落在$a$的概率是相同的，这样才能保证用这种机制所得到的样本的分布才不改变

事实上，这种假设是成立的，我们继续以上图为例子，可以求出如下所示的跳转概率，其中$P(X^{t} \in a \rightarrow X^{t+1} \in a)$表示当前样本在$a$中，下次样本也在$a$中的概率

\[\left\{\begin{matrix} P(X^{t} \in a \rightarrow X^{t+1} \in a) = \frac{a+b}{L} \\ P(X^{t} \in a \rightarrow X^{t+1} \in c) = \frac{c}{L} \\ P(X^{t} \in c \rightarrow X^{t+1} \in a)=\frac{a}{L} \\ P(X^{t} \in c \rightarrow X^{t+1} \in c)=\frac{c+b}{L} \end{matrix}\right.\]

那么

\[P(X^{t+1} \in a)=P(X^{t} \in a \rightarrow X^{t+1} \in a)P(X^{t} \in a ) + P(X^{t} \in c \rightarrow X^{t+1} \in a)P(X^{t} \in c ) \\ =\frac{a+b}{L} * \frac{a}{L} + \frac{a}{L}\frac{c}{L}=\frac{a}{L} = P(X^{t} \in a)\]

同理也有$P(X^{t+1} \in c)=P(X^{t} \in c)$成立，也就是说$P(X^{t+1})=P(X^{t})$

It's all about Sampling

采样算法の笔记