昨天实验室组会,小伙伴分享了高斯过程回归,所以赶紧我也总结一波
1. Linear Regression
线性回归问题是机器学习中最为基础的一个回归模型。线性回归使用了square loss,旨在使用一个线性函数$f(X)=X\beta$来拟合当前数据。为了简单方便,这里不考虑kernel extension的情况。其优化目标$L(Y,f(X))$和solution可以写作下式。这里假设solution $\beta$中的$X^TX$是可逆的(否则可以考虑GD的方式求解,或者做特征选择,做降维,或者考虑加入L2范数,以去掉trivial solution)。这里的$\widehat{Y}=X\beta$是响应变量$Y$在数据$X$的feature列空间下的正交投影。
\[L(Y, f(X))=(Y-X\beta)^T(Y-X\beta) \\ \beta=(X^TX)^{-1}X^TY\]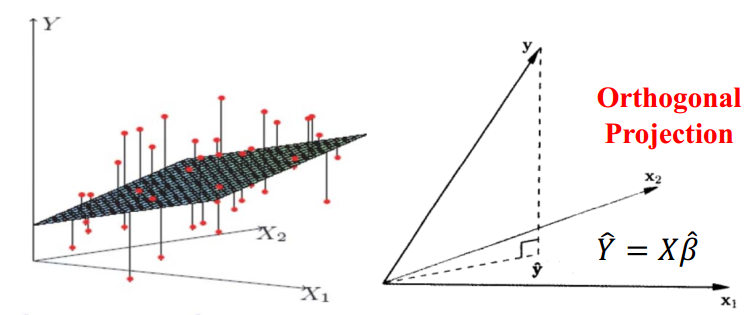
2. Bayesian Linear Regression
在前文中,线性回归主要是从优化损失函数的方式出发的。针对数据和模型,最优化的方式融合两者,旨在拿捏问题本身的一个度,而Bayesian Machine Learning则从概率的角度刻画了问题的不确定性,给出概率的解释。Bayesian ML处理问题不外乎是先验,似然,后验和推断四个方面。对于线性回归问题来说,假设数据由$y=f(x)+\varepsilon=XW+\varepsilon$方式生成,其中$\varepsilon$是高斯噪声,$\varepsilon \sim N(0, \sigma I)$。通常来说,模型参数的先验使用高斯,那么我们可以得到$y$的分布
\[W \sim N(\mu, \Sigma)\\ f \sim N(X\mu, X\sigma X^T) \\ y \sim N(X\mu, X\Sigma X^T+\sigma^2I)\]根据高斯分布的性质,可以得到参数和响应变量的联合分布。
\[P(W,y \mid X,\mu.\sigma^2,\Sigma)=N \left(\begin{bmatrix} \mu \\ X\mu \end{bmatrix},\begin{bmatrix} \Sigma & (X\Sigma)^T\\ X\Sigma & X\Sigma X^T + \sigma^2I \end{bmatrix} \right) \\ cov(y,W)=cov(XW+\varepsilon, W) = cov(XW,W)=X\Sigma\]那么,我们也可以得到参数的后验分布
\[P(W\mid X,y, \mu, \Sigma,\sigma^2)=N(\mu_W,\Sigma_W)\\ \mu_W=\mu + \Sigma X^T (X \Sigma X^T+\sigma^2I)^{-1}(y-X\mu)\\ \Sigma_W=\Sigma-\Sigma X^T(X\Sigma X^T + \sigma^2I)^{-1} X \Sigma\]一般来说,对于test data $X^0 $,我们可以采用点估计的方式,比如$W=\mu_{W}$,进行预测$f(X^0 )=X^0 \mu_{W}$。当参数的先验分布服从$N(0,s^2I)$的时候,这里后验对应的结果就等价于ridge regression 。对于预测来说,另一种方式是采用Predictive distribution,这种预测方式就约等于是把参数空间里的所有取值都取了个边,然后结合模型预测值做了一个加权平均。给定test data $X^0 $,他的predictive distribution表示为
\[P(y^0 |X,y,X^0 ,\mu,\Sigma,\sigma^2)\\ =\int P(y^0 \mid W, X^0 , \sigma^2)P(W \mid X,y,\mu,\Sigma,\sigma^2)dW\\ =N(X^0 \mu_W,X^0 \Sigma_W (X^0 )^T+\sigma^2I)\]幸运的是,对于高斯分布来说,他的predictive distribution也是一个高斯。有趣的是,对于这个问题,点估计的结果和predictive distribution的预测结果都是一样的,但是predictive distribution还可以给出预测的方差,作为预测结果的置信度,这一方面是点估计做不到的。
3. Gaussian Process Regression
GPR可以算作是比贝叶斯线性回归更加general的一个模型。GPR是说,与其想参数$W$的先验,不如就直接想回归函数的先验分布。所以GPR的先验不是定义在参数上,而是模型本身。那么为啥不直接考虑参数$W$的先验呢?原因是我们模型$f$是潜在的无穷维度的,而以前的方式在有限维度上work。所以大牛们说:The Gaussian process is a natural generalization of the multivariate Gaussian distribution to potentially infinite settings
对于GP的正式定义,这里就不写(抄)了。简单来说,GP可以由mean function $\mu(X)$和covariance function(或者叫kernel) $K(X,X)$唯一确定。可以写成:
\(P(f\mid X)=N(\mu(X),K(X,X))\) 其中,
- mean function度量了函数的central tendency,一般来说是一个常数,比如0。当然也可以用其他函数,考虑到会引入额外参数,一般0是比较常用的选择
- kernel表达了我们希望function具有的性质和形状,比如常用的高斯径向基核函数就想要靠的近的点有相似的函数值
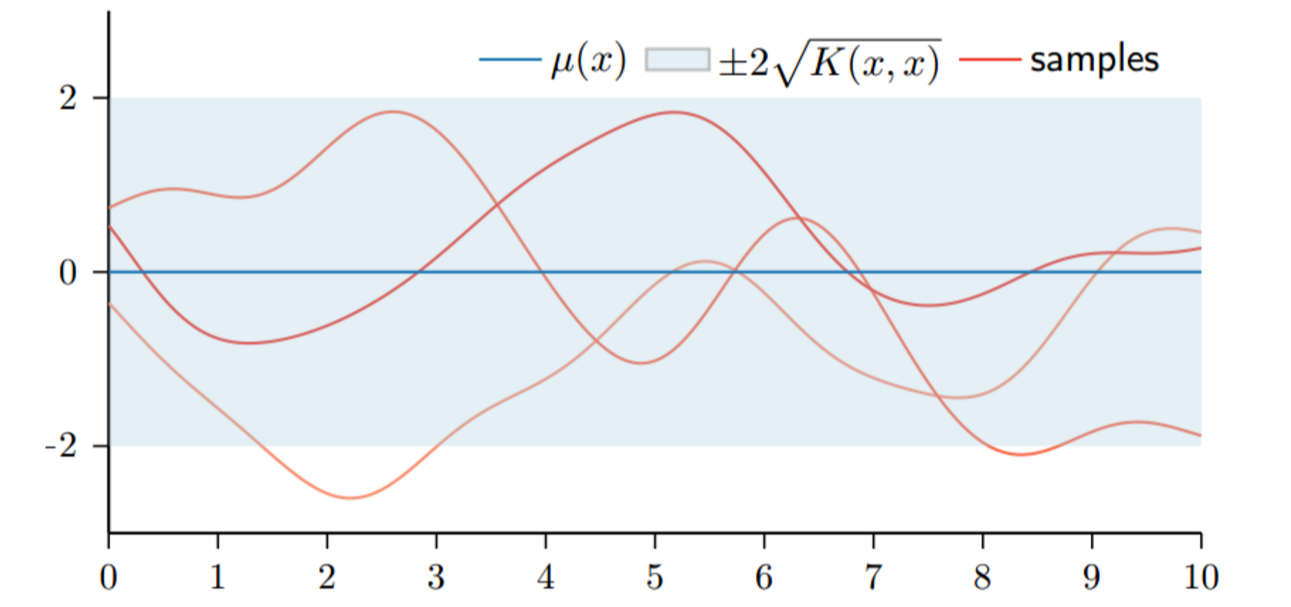
下图是一个GP的采样例子,横轴是x,纵轴是取值。给定一个$x_{1}$,它对应的mean function和kernel都唯一确定,那么这个点处的分布也确定,那么就可以根据这个分布采样了,然后对于下一个数据$x_{2}$,我们需要在已知$x_{1}$的时候,计算条件分布,然后采样,依次类推。这个过程其实就是在预测数据
那么GPR是怎么预测数据的呢?这个过程和之前的Bayesian Linear Regression类似,是从联合概率推后验概率。给定已有的训练数据$X$,回归值$f$ 和test data $X^0 $,我们要求预测值$f^0 =f(X^0 )$。那么联合概率可以表示为:
\[P(f,f^0 )=N \left(\begin{bmatrix} \mu(X) \\ X\mu(X^0 ) \end{bmatrix},\begin{bmatrix} K(X,X) & K(X,X^0 )\\ K(X^0 ,X) & K(X^0 ,X^0 ) \end{bmatrix} \right)\] 那么,进一步得到条件概率的形式。需要一说的是,GPR也是可以考虑noise的情况的,这里没有再做推导,具体方法可以参考Bayesian Linear Regression。(下面的公式中的$K^{-1}=K(X, X)^{-1}$,或者考虑有高斯noise,$K^{-1}=(K(X, X)+\sigma^2I)^{-1}$)。这个解的形式,和之前的Bayesian Ridge Regression的形式是很相似的,实际上,当mean function等于0,kernel取值$K=XX^T$的时候,两个模型是等价的
\[P(f^0 \mid X^0 , X,f)=N(\mu_{0}(X^0 ),K_{0}(X^0 ,X^0 ))\\ \mu_{0}(X^0 )=\mu(X^0 )+K(X^0 ,X)K^{-1}(f-\mu(X))\\ K_{0}(X^0 ,X^0 )=K(X,X^0 )-K(X^0 ,X)K^{-1}K(X,X^0 )\] 事实上,对于GP来说,他的后验均值可以看做是weighted combination of kernel function ,这里的weight $\alpha_{i}=K(X,X)^{-1}(f(X_{i}-\mu(X_{i})))$
\[\mu_{0}(X^0 )=\mu(X^0 )+K(X^0 ,X)K^{-1}(f-\mu(X))\\ =\mu(X^0 ) + \sum^N_{i=1} \alpha_iK(X_i,X^0 )\]有了条件分布的形式,那么就可以给出采样,或者说预测的图
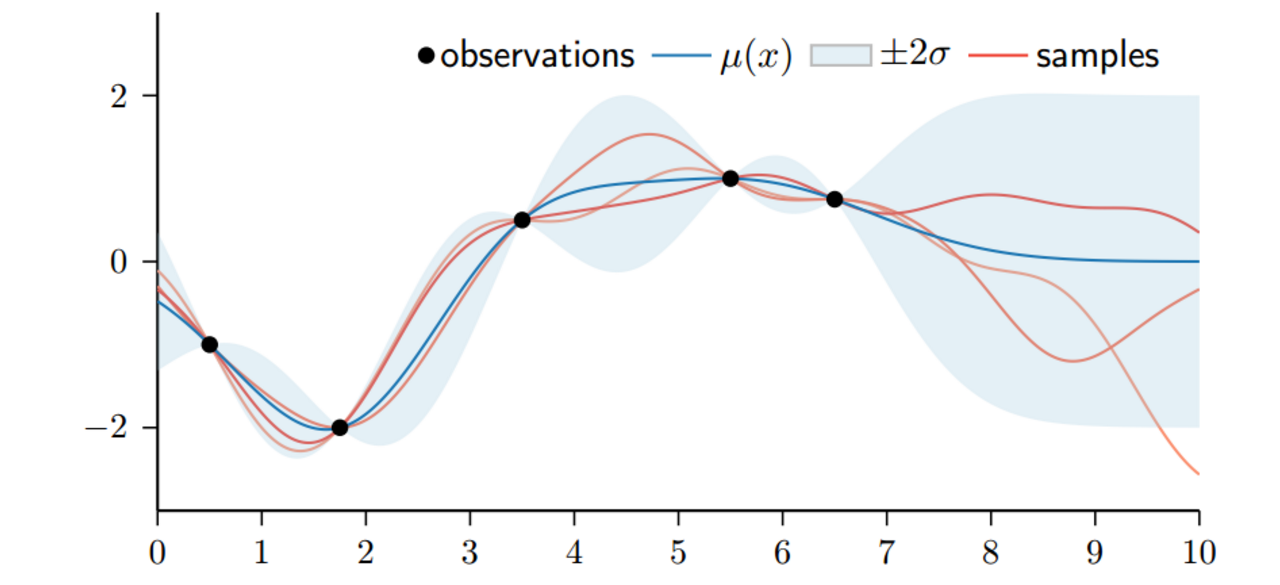
注意到图里有阴影部分,这个是表示预测的方差(置信度)。对于存在数据的地方,预测方差很小,否则不确定性越大。这里也是GPR有一个优于贝叶斯线性回归的地方,GPR的后验分布直接能给出预测方差,而不需要借助predictive distribution遍历参数空间做一个加权和。当然GPR的求解会涉及到(增量式)矩阵求逆,这个操作是很耗时的,是GPR的一个大bug。
4. Hyper-parameters of GPR
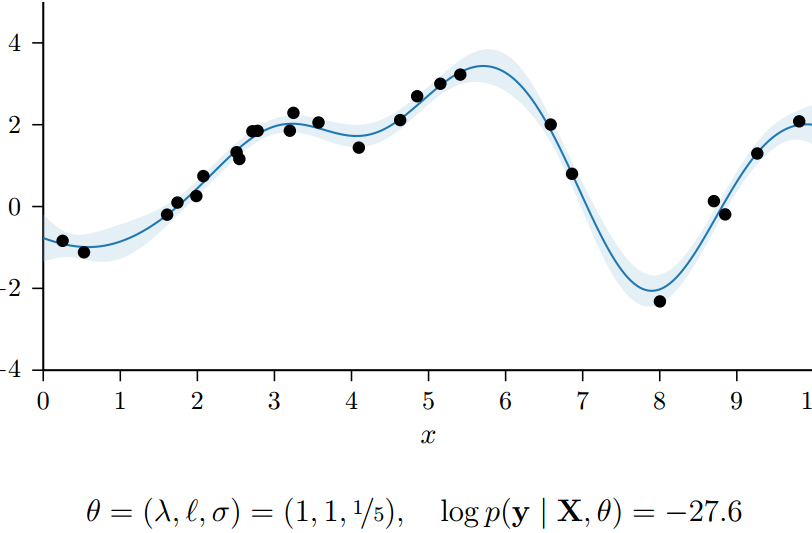
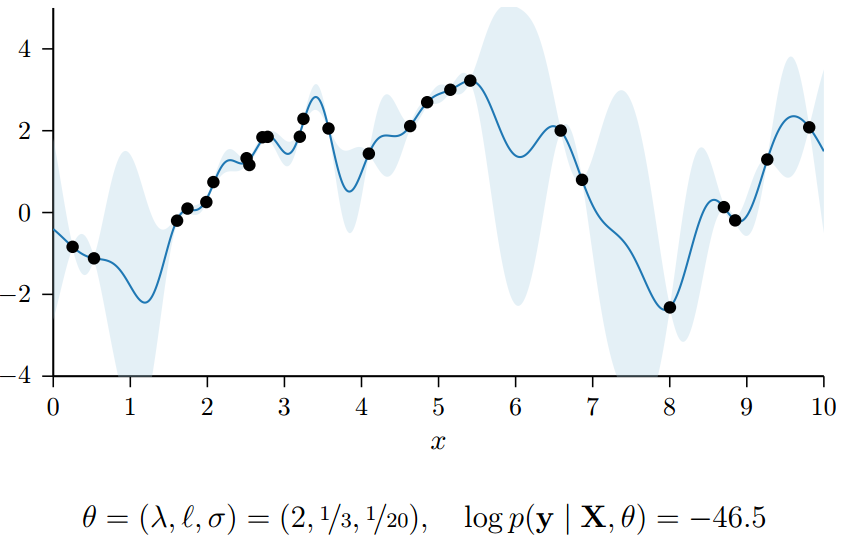
GP的kernel选择有很多,可以是周期性的,也可以是非周期性的。但是核都是有参数的。所以对于GPR来说,参数来自于kernel和mean function。一般考虑mean function=0,那么模型参数来自于kernel function,比如length scale, the output scale, and the noise variance,现在把参数统记为$\theta$。为了要学习超参,需要使用marginal likelihood,他是用来度量在给定先验的情况下,拟合数据的好坏层度。
\[P(y\mid X,\theta)=\int P(y\mid f)P(f\mid X, \theta)df\]积分式子里的第一项是iid的noise term(这里假设$y=f(X)+noise$),第二项是一个GP先验。marginal likelihood针对未知的GPR输出值$f$做了一个marginalization。在给定参数$\theta$下,模型的先验分布就确定了,marginal likelihood从而衡量了给定超参时,整个先验空间对数据的拟合能力。前文说过,这样两个高斯相乘之后的积分仍然是高斯的:
\[P(y\mid X,\theta)=N(\mu(X;\theta),K(X,X;\theta)+\sigma^2I)\]一般来说,会使用$log P(y\mid X,\theta)$来作为一个超参好坏的度量。令$V=K(X,X;\theta)+\sigma^2I$
\[log P(y \mid X, \theta)=-\frac{(y-\mu)^TV^{-1}(y-\mu)}{2}-\frac{log\mbox{ } detV}{2} -\frac{Nlog2\pi}{2}\]其中,
- 第一项代表了data fitness。是在V度量下的距离度量(均值和真实值y),所有距离越小越好,然后还有个负号,所以越大越好
- 第二项是Occam’s razor,有负号,所以也是越大越好。等价于det V越小越好,由于噪声的方差实际中没法控制,所以,考虑gp的方差越小越好,模型变化范围小,能表达数据的能力小,模型趋于简单。
- 最后当然是数据越多越好了
总的来说,log marginal likelihood越大越好。下面的两个图,是在kernel为$K=\lambda^2exp(\frac{\mid \mid x-x’ \mid \mid^2}{2l^2})$的时候,模型在不同超参下的,marginal likelihood的大小。