10. Model-based RL

上一章说的是Model-based Planning，即结合已知的dynamics，做出更好的value function的估计和更好的决策。本章的Model-based RL 是指，dynamics未知（本文特指状态转移，好像现在对reward function都不会怎么学习？reward都是专业知识？），但是我们要去学习它！学习到之后，我们又可以做planning啦。model-based RL和model-free RL的区别就是前者是去学习dynamics，然后获得value function或者policy，后者是直接去学习value function或者policy，而不依赖dynamics。所以model-based RL可以用下面的图表示，这里的地球是一个卡通图案，表示他是我们通过样本学习到的dynamics，然后整个RL过程就在这样的已知的dynamics中进行。

下面是一个model-based RL的流程图：一开始我们初始化一定的policy，用他和环境交互，获得经验数据；在使用这个经验数据学习出dynamics。当dynamics已知的时候，我们就可以planning出更好的policy。比如使用动态规划planning（policy iteration, value iteration, MC, TD等等），Stochastic optimization，MCTS等model-based planning的方法。但是，这种相互依赖的loop，一好则好，一旦学习有猜错，那就开始累计了。实际效果会限制于所学习的model/dynamics的好坏。因此，如果model学得太烂，完全就可以用model-free等等的方式

10.1 Planning with learned dynamics

从上面的示意图，只能看出model-based RL由三个步骤组成：

用当前的policy/value，出招，得到一些反馈数据
根据反馈数据，学习出一个dynamics $f$
根据$f$来planning，优化policy/value

在实际操作中，会有一些其他问题：训练数据是否足够用来学习，是否能学习到一个好的模型？

10.1.1 Distribution mismatch

训练数据是源于真实的MDP，但是训练数据是否能很好的反应MDP，这是未知的。比如在自动驾驶问题中，如果车子一直都在左转弯绕圈，那么用这样的数据所学习的planning，不就只能左转弯了么。实际上训练数据（左转绕圈）和真实驾车场景是不一样的。如果我们用于学习dynamics的算法很厉害，拟合能力很强，那么这个问题就会更加突出，因为学到的dynamics overfits，建立在它之上的planning也就不会好。

解决这个问题的一个可行方案就是扩充训练数据集，竟可能的去避免mismatch。如下所示，在第4步增加数据扩充的步骤。

这个策略和模仿学习(imitation learning)中的DAgger算法（Dataset Aggregation）很相似（伪代码如下），对于DAgger算法的dabug就是要人来打标签，选动作。而在强化学习中，则是直接使用当前policy的动作值当label，勉强人工的过程。

但是，这个扩充数据集的方法就不适用于open loop plan了，毕竟没有交互，就没机会得到新数据。

10.1.2 Model error

另一个问题就是，真实的dynamics我们是不知道的。通过学习出来的dynamics很有可能是不准确的，甚至是有大bug的。比如在自动驾驶问题中，如果dynamics学得不好，在给定状态下做的planning，也许会给出错误的答案：如果学习到的dynamics告诉你前面是个左转弯（实际上是直路），那么planning会告诉你赶紧左转，但是一旦左转，那就会冲出公路咯。

这种情况下，除了数据扩充的方法外，还可以re-planning。在一段时间之后的新状态下，进行重新planning，一旦re-planing的结果发现不能再左转了（即使学习到的dynamics告诉你应该要左转），这个时候还是有改正的机会。

下面代码的第3就是re-planning（注意，之前的代码是每N次，更新一次dynamics，然后做一次planning，这里是每N次，更新一次dynamics，但是planning是做了N次的）

但是这里re-planning带来的计算量不会太恶心，因为如果每次都在做planning的话，其实不用去plan那些时间片很久以后的事，往往plan一个短期的future就很work了，这时候就可以使用上一章提到的Stochastic optimization方法了。

10.2 Learn a model by supervised learning

为了要学习dynamics（这里特指状态转移和reward function），可以求助由于监督学习。给定训练数据${s_{t},a_{t},r_{t+1},s_{t+1}}^n$，我们要求解的是$s_{t+1}=P(S_{t+1}\mid S_{t},A_{t})$和$r_{t+1}=R(R_{t+1}\mid S_{t},A_{t})$。这时候监督学习学习的目标不在是label，而是输入$s_{t},a_{t}$，输出$s_{t+1}$和$r_{t+1}$。回想最开始我们提到的动态系统，就可以用来解他们，而且还是考虑到了数据之间的依赖情况。当然，我们也可以把这种依赖情况忽略，之间采用简单的模型去拟合：

\[s_1,a_1 \rightarrow r_2,s_2\\ s_2,a_2 \rightarrow r_3,s_3\\ ...\\ s_{T-1},a_{T-1} \rightarrow r_{T},s_{T}\\\]

比如用回归问题来集合reward，用密度估计来拟合state。总的来说，可以用local和global两个大类的模型来拟合（比如下列）。global模型是指用一个模型来拟合所有的state和action的输出，local模型则是用多个局部的小模型来拟合特定状态和action下的输出。

Table Lookup Model
Linear Expectation model
linear gaussian
gaussian process
deep belief network
iLQR等等

10.2.1 Fitting global dynamic model

10.2.1.1 Table Lookup Model

table lookup其实就是通过简单的数据统计，记录所有相同输入下的输出均值。可以将它视作一个全空间下的KNN回归模型，这个K等于数据点的个数。

\[\widehat{P}_{ss'}^a=\frac{1}{N(s,a)}\sum_{t=1}^n1(S_t,A_t,S_{t+1}=s,a,s')\\ \widehat{R}_{s}^a=\frac{1}{N(s,a)}\sum_{t=1}^n1(S_t,A_t=s,a)R_t\]

当然，这种基于表格的方式，仅仅适用于离散且维度不大的情况。并且模型的泛化能力依赖于训练数据，如果，缺少某个状态下的训练数据，那么模型肯定是学习不到这个状态的。在学习出model之后，就可以使用planning了。在model-based RL中还有一个特别的planning方法，叫做Sample-based Planning。这种方法简单有效。它先通过训练数据学习出一个模型，然后使用这个模型再模拟/采用出更多的样本，最后再使用model-free的方法（比如Q-learning, sarsa, MC等等）求出policy或者value function。比如给定state空间是{A,B}和训练episode数据（state, reward）：

\[A,0,B,0\\ B,1\\ B,1\\ B,1\\ B,1\\ B,1\\ B,1\\ B,0\]

我们可以通过table lookup的方法，得到下面的dynamics

那么，如果使用sample-based planning方法，我们需要对这个dynamics就行采样，比如得到一些采样episode：

\[B,1\\ B,0\\ B,1\\ A,0,B,1\\ B,1\\ A,0,B,1\\ B,1\\ B,0\]

最后，我们便可以在采样数据上使用model-free的方法学习policy或者value了，比如使用MC的方法（用episode的return来近似）可以得到$V(A)=1,V(B)=0.75$。一个随之而来的问题就是，采样数据不一定可靠（取决于所学习到的model），那为什么结合训练数据一起使用呢？可以的，这就是Dyna算法

10.2.1.2 Dyna

既然我们有了来源于真实MDP的数据和源于学习到的MDP的数据，那么自然我们可以把他们合起来，学习一个更好的policy或者value function。Dyna就是这样的算法，他的思想可以用下面的图表示：

Dyna如果建立上sample-based planning方法上，那么采样的数据将用于planning，这里planning选用的是model-free的q-learning，真实的数据也是通过Q-learning来更新value function。具体来说dyna的伪代码如下：

第d步用真实数据更新value，e步学习dynamics，f步则是planning。Dyna的步骤很简单，而且效果也很好

10.2.2 Fitting local dynamic model

要找到一个global model来很好的拟合所有state和action是非常困难的，这样学到的模型本身也是非常复杂的，对于有效task来说，dynamics本身会比policy要复杂。如果要用RL来做红绿灯控制，那么去学习该路口（和其附近）的路况，一定比学习我国所有道路的路况，要容易而且有效很多。这时候，local model就会比较好。

10.2.2.1 Fit with iLQR

在上一章的trajectory optimization部分介绍的LQR/iLRQ就可以用作一个local model

\[\min_{a_1,... ,a_T} \sum_{t=1}^T c(s_t,a_t) \mbox{ s.t. } s_t=f(s_{t-1},a_{t-1})\\ \min_{a_1,... ,a_T} c(s_1,a_1) + c(f(s_1,a_1),a_2)+...+c(f(f(...)),a_T)\]

比如，我们假设使用linear model $f(s_{t},a_{t})\approx w_{t}s_{t}+b_{t}a_{t}$来拟合每一个local dynamics，还可以在考虑高斯noise，$P(s_{t+1}\mid s_{t},a_{t})=N(f(s_{t},a_{t}),\Sigma)$。这样在LQR中，每次迭代他都反馈回来一个线性的dynamics（x就是s，u就是a）。

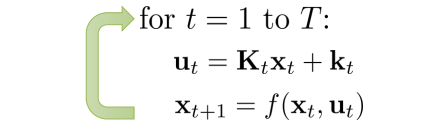
所以，我们可以使用他来快速找到local dynamics

在这个设定下，图中的fit dynamics就是指去求解f中的参数w和b了，图中的$p(a_{t}\mid s_{t})$可以取不同的值

使用iLQR：

\[p(a_{t}\mid s_{t})=\delta(a_{t}=K_{t}(s_{t}-\widehat{s}_{t})+k_{t}+\widehat{a}_{t})\]

考虑noise：

\[p(a_{t}\mid s_{t})=N(K_{t}(s_{t}-\widehat{s}_{t})+k_{t}+\widehat{a}_{t}, \Sigma_{t})\]

其中$\Sigma_{t}=Q_{a_{t},a_{t}}^{-1}$是一个推荐取值。因为在iLQR中，如果变化动作a，导致Q（这里的Q表示cost to go，不是reward to go）变化很大的话，$Q_{aa}$的值也会变得很大。这时候表示动作a的选择比较敏感。

10.2.2.2 Local model is too local

然而，local model的问题在于，local model没有普适性，local information只适用于local。比如下面的图，蓝色实线是学习到的local linear dynamics，绿线是真实的。如果一直使用蓝色实线所planning到的policy来走的话，可能会越走越错（蓝色虚线是planning的预想结果，红色虚线是真实执行的结果）。产生这样的原因就是local model overfits local state。

对于这个问题来说，如果我们约束trajectory distribution都分布得比价紧密，那么local dynamics之间也会变得比较紧密

这里trajectory的分布是通过KL散度来衡量的。其中H函数表示熵

\[D_{KL}(P(\tau)\mid\mid \widehat{P}(\tau))=E_{P(\tau)}\left[ \sum_{t=1}^T logP(a_t\mid s_t) -log\widehat{P}(a_t\mid s_t)\right]\\ =\sum_{t=1}^TE_{p(s_t,a_t)} \left[ logP(a_t\mid s_t) -log\widehat{P}(a_t\mid s_t)\right]\\ =\sum_{t=1}^TE_{p(s_t,a_t)} \left[ -log\widehat{P}(a_t\mid s_t) - H(P(a_t\mid s_t))\right]\]

那么，结合KL散度的约束，可以写成下面的优化问题

\[\min_P \sum_{t=1}^T E_{P(s_t,a_t)}[c(s_t,a_t)] \mbox{ s.t. } D_{KL}(P(\tau)\mid\mid \widehat{P}(\tau)) \leq \epsilon\]

这个问题可以通过dual gradient descent来求解。下图的L函数表示拉格朗日

对于第一步的求解，即：

\[\min_P \sum_{t=1}^T E_{P(s_t,a_t)}[c(s_t,a_t) - \lambda log\widehat{P}(a_t\mid s_t) - \lambda H(P(a_t\mid s_t))] -\lambda \epsilon\]

它的求解要用到iLQR的一个等价理论：iLQR在高斯噪声下的优化问题等价于下式：

\[\min_P \sum_{t=1}^T E_{P(s_t,a_t)}[c(s_t,a_t) - H(P(a_t\mid s_t))]\]

所以，dual gradient descent的第一步可以通过令$\widehat{c}(s_{t},a_{t})=\frac{1}{\lambda}c(s_{t},a_{t})-log\widehat{P}(a_{t}\mid s_{t})$，然后通过iLQR来求解

最后，local和global的方法也可以合起来用，比如用贝叶斯模型来拟合local model，把global model以先验的形式加入。

10.3 Learn model and policy

model-based planning太慢（比如要做数据曾广，要做re-planning等等），难以给出实时响应，所以还是直接用policy比较好。比如打羽毛球时先根据环境和羽毛球的速度角度等等，planning一下落球点，然后跑过去接球。这个过程如果能得到一个好的接球policy的话，那么以后别人扔飞盘，就能不用重新planning一下，才能接了。所以policy隐含有更好的泛化能力。如果，我们能知道dynamics，那么整个序列决策过程可以用下图表示，那么就可以像deep model一样做back propagation

实际上，这个问题和前面的trajectory optimization相关，但是难度加大了。因为这里引入了policy，而policy把各个状态转换紧密耦合在一起了。所以需要在做planning的时候，还学习policy。或者说是有指向性的planning出一些样本，来引导policy的学习，也就是guided policy search。在加入policy之后，整个问题在trajectory optimization的基础上，变成了constrained trajectory optimization

\[\min_{a_1,... ,a_T,s_1,...,s_T, \theta} \sum_{t=1}^T c(s_t,a_t) \mbox{ s.t. } s_t=f(s_{t-1},a_{t-1}), a_t=\pi_\theta(s_t)\\ \mbox{简化：}\min_{\tau, \theta} c(\tau) \mbox{ s.t. } a_t=\pi_\theta(s_t)\]

上面的问题可以通过增广拉格朗日法+dual gradient descent来解。使用曾广拉格朗日的原因是为了通过L2项来增加求解的稳定性。下面伪代码中的$L$就是增广拉格朗日。

\[L(\tau,\theta,\lambda)=c(\tau)+\sum_{t=1}^T\lambda_t(\pi_\theta(s_t)-a_t) + \sum_{t=1}^T\delta_t(\pi_\theta(s_t)-a_t) ^2\]

伪代码中的第二步，在求解policy的时候，已经不再是紧耦合的了，而是一个普通iid的监督学习，这就方便优化求解了。整个过程可以看做是一个guided policy search，第一步planning出最好的样本，然后将这个样本用于引导policy有更好的更新。当然这个过程也可以在多个trajectory之间并行，因为一条trajectory引导得到的policy，它的泛化性能还不高。比如，policy只适用于从一个state出发的情况。一个好的policy，无论从迷宫的那个地方进入，都要走得出去才可以。下图就是一个multiple trajectory的示意图，叉就是目标task，其他的表示不同的trajectory。

这时候的目标变成：

\[\min_{\tau_1,...,\tau_N, \theta} \sum_{i=1}^N c(\tau_i) \mbox{ s.t. } a_{t,i}=\pi_\theta(s_{t,i})\]

这里可以在第一步里并行求解（分布式机器学习还是很有用的）

11. Soft optimality, Inference and Control

我们在一开始引入强化学习的时候，就说强化学习是建立在Reward Hypothesis之上的：所有的RL task都可以通过最大化累计reward的方式来实现。所以无论是通过deterministic policy或者是Stochastic policy，RL都想要找出一个最好的策略（arg max）

\[a_1,...,a_T=\arg\max_{a_1,...,a_T}\sum^T_{t=1} \gamma^{t-1}r(s_t,a_t) \mbox{ s.t. }s_{t+1}=f(s_t,a_t)\\ \pi=\arg\max E_{s_{t+1}\sim P(s_{t+1}\mid s_t,a_t),a_t\sim \pi(a_t \mid s_t)}[\gamma^{t-1}r(s_t,a_t)]\]

但是，这种方式并不能完全刻画人类的真实行为。人类真实行为含有随机性，它往往是次优的。以下图为例，如果我们需要从一个地方跑去另一个地方，当然两点之间线段最短，所以最优的方案是走黑色的直线。但是相比于人，猴子却有可能走其他的方案（图中曲线），同样也能到达目的地。这些方案虽然本身并不是最优，但是他们所带来的累计reward可能与黑线的差异并不大。因此，我们更希望去刻画这种带有随机性的次优行为，也就是Soft optimality。这种随机性会导致行为选择不是最优的，带来一定mistake，但是，只要最后能较好的完成task，这些mistake也是可容忍的。在这个例子里，猴子真的不会关心要不要走直线，只要能（较快地）到达目的地就行了。最后，这种随机性的出现，也增大了exploration的机会，RL也会更加的鲁棒。

11.1 Soft optimality and PGM

为了刻画这种行为，之前的那些argmax的方法就不太适用了。因为模型需要保证能以一定的概率选中次优的动作，并且也要能尽量最大化累计reward。对于这种以概率的序列决策过程，可以采用PGM，也就是概率图模型（Probabilistic Graphical Model），对于RL来说，PGM是长成这样的：

PGM常常是用阴影的圆表示已观察值，空心表示未知变量（也就是state和action）。这里的变量$O$表示agent的goal或者intention。比如可以让$O$是0/1取值，表示猴子是不是想要接近目的地。是就$O_{t}=1$，否则是0。如此，我们便可以使用$P(\tau \mid O_{1:T})$表示在猴子为了要达到一定goal的条件下，这条trajectory的概率是多少。

对于这个式子，可以使用贝叶斯公式展开。第三个公式是对上面的PGM用了马尔科夫的条件独立性。给定$\tau$，$O_{t}$是相互条件独立的。并且对于单个的$O_{t}$可以通过父节点（$s_{t},a_{t}$）确定。

\[P(\tau \mid O_{1:T})=\frac{P(\tau)P(O_{1:T}\mid \tau)}{P(O_{1:T})} \propto P(\tau) \prod_t P(O_t \mid s_t,a_t)\]

一般来说，会取值$P(O_{t}\mid s_{t},a_{t}) \propto exp(r(s_{t},a_{t}))$。这样带入上式，可以得到下式。这个式子的含义就是我们会倾向于去选择那些累计reward大，并且出现概率高的trajectory $\tau$。由于$P(\tau \mid O_{1:T})$是一个概率，所以，如果还有别的trajectory，它的累计reward也比较大，出现概率也比较高的话，那么它也可能被选中，也就达到了soft optimality的目的。

\[P(\tau \mid O_{1:T}) \propto P(\tau) exp(\sum_t r(s_t,a_t))\]

那么问题来了，怎么求解？在PGM中，这种给定观测值，求解隐变量的后验分布的问题叫做inference（可以回想HMM的例子，在给定观察值下，去求解state）。在本文中，inference分为三个部分

计算backward message $\beta_{t}(s_{t},a_{t})=P(O_{t:T}\mid s_{t}, a_{t})$
计算policy $P(a_{t} \mid s_{t}, O_{1:T})$
计算forward message $\alpha_{t}(s_{t})=P(s_{t}\mid O_{1:t-1})$

11.2 Inference

后面的推到会用到这个PGM的结构，所以放这里方便查阅

11.2.1 Backword message

从backward message $\beta_{t}(s_{t},a_{t})=P(O_{t:T}\mid s_{t}, a_{t})$的形式可以得到一些信息：比如当t=1时刻，给定s1,a1，$O_{1}$和$S_{2}$是条件独立的，$O_{1}$和$O_{2:T}$也是条件独立的。也就是说：

\[\beta_{t}(s_{t},a_{t})=P(O_{t:T}\mid s_{t}, a_{t})=P(O_t\mid s_t,a_t)P(O_{t+1:T}\mid s_t,a_t)\]

而$P(O_{t}\mid s_{t},a_{t}) \propto exp(r(s_{t},a_{t}))$是已知的。所以我们的策略就是通过引入下一时刻的$s,a$，使得分解出更多的$P(O_{t}\mid s_{t},a_{t})$。所以有：

\[\beta_{t}(s_{t},a_{t})=P(O_{t:T}\mid s_{t}, a_{t})=\int P(O_{t:T}, s_{t+1}\mid s_{t}, a_{t}) ds_{t+1}\\ =\int P(O_t,O_{t+1:T}, s_{t+1}\mid s_{t}, a_{t}) ds_{t+1} \\ =\int P(O_{t+1:T}\mid s_{t+1})P(s_{t+1}\mid s_{t}, a_{t}) P(O_t\mid s_t,a_t) ds_{t+1}\\ =P(O_t\mid s_t,a_t)\int P(O_{t+1:T}\mid s_{t+1})P(s_{t+1}\mid s_{t}, a_{t}) ds_{t+1}\]

上面的式子，第二项是dynamics，第三项$P(O_{t}\mid s_{t},a_{t}) \propto exp(r(s_{t},a_{t}))$。我们把第一项$P(O_{t+1:T}\mid s_{t+1})$，令为$\beta_{t+1}(S_{t+1})$。我们继续把下一时刻的a加进去：

\[P(O_{t+1:T}\mid s_{t+1})=\int P(O_{t+1:T},a_{t+1}\mid s_{t+1}) da_{t+1}\\ =\int P(O_{t+1:T}\mid s_{t+1},a_{t+1})P(a_{t+1}\mid s_{t+1}) da_{t+1}\]

积分里的第一项就是下一时刻的backward message $\beta_{t+1}(s_{t+1},a_{t+1})$。而第二项$P(a_{t+1}\mid s_{t+1})$，他看起来像个policy，但是它不是task-oritented，所以在这里，他不是policy。或者说，他是一个policy priori，因为他没有goal，仅仅是说在某个状态下，可能采取的action分布是啥，因此完全可以认为他是一个uniform Distribution，取一个定值。

因此，我们可以倒着求出$\beta$的值。注意$\beta_{T}(s_{T},a_{T})=P(O_{T}\mid s_{T},a_{T})\propto exp(r(s_{T},a_{T}))$

这个更新过程看起来很繁琐，其实，如果做一个变量替换，就会有一些不得了的发现。现在令：

\[V_t(s_t)=\log \beta_t(s_t)\\ Q_t(s_t,a_t)=\log\beta_t(s_t,a_t)\]

那么结合$\beta_{t}(s_{t})=\int P(a_{t}\mid s_{t})\beta_{t}(s_{t},a_{t})da_{t}$，可以得到下面这个神奇的式子：

\[V_t(s_t)=\log \int P(a_t \mid s_t) \exp(Q_t(s_t,a_t))da_{t}=\log \int \exp(\log P(a_t \mid s_t) + Q_t(s_t,a_t))da_{t}\\ Q_t(s_t,a_t)=r(s_t,a_t)+\log E_{s_{t+1} \sim P(s_{t+1}\mid s_t,a_t)}[exp(V_{t+1}(s_{t+1}))]\]

第一个式子的神奇之处就在于，他可以视作一个Soft max（不是神经网络里的softmax），是一种松弛的，用来求最大化的算子。在$Q_{t}(s_{t},a_{t})$变得很大的时候，$V_{t}(s_{t}) \rightarrow \max_{a_{t}}Q_{t}(s_{t},a_{t})$（注意，这里仍然假设$P(a_{t}\mid s_{t})$是uniform distribution。如果假设他是uniform的话，那么可以把$P(a_{t}\mid s_{t})$看做是reward的一部分：$\widehat{r}(s_{t},a_{t})=r(s_{t},a_{t})+\log P(a_{t}\mid s_{t})$）。
对于第二个式子来说
1. 考虑deterministic transition的情况，就可以把期望用一个确定的转移状态替换：
  \[Q_t(s_t,a_t)=r(s_t,a_t)+V_{t+1}(s_{t+1})\]
2. 有其他理论工作进一步可以将式子2改成下式：
\[Q_t(s_t,a_t)=r(s_t,a_t)+E[V_{t+1}(s_{t+1})]\]

整个backward message的计算过程就很像value iteration了。它先计算Q，然后对Q取soft max 来得到V。而value iteration则是直接最大化Q

最后，以上的推到都基本没有考虑discount factor，但是也是可以加上去的，比如：

\[Q_t(s_t,a_t)=r(s_t,a_t)+\gamma E[V_{t+1}(s_{t+1})]\]

另一个比较好的改进是加入explicit temperature $\alpha$。当$\alpha \rightarrow 0$的时候，这个soft max就无限接近于hard max了

\[V_t(s_t)=\alpha \log \int \exp( \frac{\log P(a_t \mid s_t) + Q_t(s_t,a_t)}{\alpha})da_{t}\]

11.2.2 policy

对于policy $\pi(a_{t} \mid s_{t})=P(a_{t} \mid s_{t}, O_{1:T})$的计算，只用贝叶斯方法就行了

\[\pi(a_{t} \mid s_{t})=P(a_{t} \mid s_{t}, O_{1:T})=\frac{P(a_t , s_t \mid O_{1:T})}{P(s_t\mid O_{1:T})}\\ =\frac{P(O_{1:T} \mid a_t,s_t)P(a_t,s_t)/P(O_{1:T})}{P( O_{1:T}\mid s_t)P(s_t)/P(O_{1:T})}\\ =\frac{\beta_t(s_t,a_t)}{\beta_t(s_t)}P(a_t|s_t)\]

这里仍然假设$P(a_{t}\mid s_{t})$是uniform的，所以进一步推得到policy其实是一个指数加权的advance function。他的含义就是，soft optimality是选择那些好于“平均水平”的动作，而不是单纯的选能最大化advance的动作。动作的选择概率等价于到底这些动作要好于平均多少（需要提前归一化成概率值）。

\[\pi(a_{t} \mid s_{t})=\frac{\beta_t(s_t,a_t)}{\beta_t(s_t)}=\exp(Q_t(s_t,a_t)-V_t(s_t))=\exp(A_t(s_t,a_t))\]

考虑到explicit temperature。当$\alpha \rightarrow 0$的时候，就趋近于做的是greedy policy

\[\pi(a_{t} \mid s_{t})=\exp(\frac{Q_t(s_t,a_t)-V_t(s_t)}{\alpha})=\exp(A_t(s_t,a_t)/\alpha)\]

11.2.3 forward mesage

最后来看forword message $\alpha_{t}(s_{t})=P(s_{t}\mid O_{1:t-1})$的计算（注$\alpha_{1}(s_{1})=P(s_{1})$，通常来说，初始状态是知道的）。

\[\alpha_{t}(s_{t})=P(s_{t}\mid O_{1:t-1})=\int P(s_t,s_{t-1},a_{t-1}\mid O_{1:t-1})ds_{t-1}da_{t-1}\\ =\int P(s_{t}\mid s_{t-1},a_{t-1})P(a_{t-1}\mid s_{t-1},O_{t-1})P(s_{t-1}\mid O_{1:t-2})ds_{t-1}da_{t-1}\]

积分式子里的第一项是dynamics，第三项是$\alpha_{t-1}(s_{t-1})$，对于第二项来说：

\[P(a_{t-1}\mid s_{t-1},O_{t-1})=\frac{P(O_{t-1}\mid s_{t-1},a_{t-1})P(a_{t-1}\mid s_{t-1})}{P(O_{t-1} \mid s_{t-1})}\]

对于这个式子，分子的第一项$P(O_{t-1}\mid s_{t-1},a_{t-1}) \propto \exp(r(s_{t-1},a_{t-1}))$，第二项如果仍然假设是uniform的，这时候分母是$P(O_{t-1}\mid s_{t-1},a_{t-1}) )$的一个normalization。所以：

\[\alpha_{t}(s_{t})=P(s_{t}\mid O_{1:t-1}) \\ \propto \int P(s_{t}\mid s_{t-1},a_{t-1}) \exp(r(s_{t-1},a_{t-1}))\alpha_{t-1}(s_{t-1})ds_{t-1}da_{t-1}\]

11.2.4 Inference in action

最终我们要求解的是$P(s_{t}\mid O_{1:T})$。他可以通过前后向message得到：

\[P(s_{t}\mid O_{1:T})=\frac{P(s_t,O_{1:T})}{P(O_{1:T})}=\frac{P(O_{t:T}\mid s_{t})P(s_t,O_{1:t-1})}{P(O_{1:T})}\\ \propto \beta_t(s_t)\alpha_t(s_t) P(O_{1:t-1}) \propto \beta_t(s_t)\alpha_t(s_t)\]

从下面的示意图可以看出：

前向信息$\alpha_{t}(s_{t})=P(s_{t}\mid O_{1:t-1})$表示观察到t-1时刻之前的intention，能到达到$s_{t}$状态的概率是多少（intention观察到越多，也就下一时刻的状态能被推测出的概率也就越大（前提是为了要接近目的地而设置的reward）。图右端大，左边窄）。
后向信息$\beta_{t}(s_{t},a_{t})=P(O_{t:T}\mid s_{t}, a_{t})$表示从给定时刻t开始，完成goal的概率是多少（图左端大，右边窄）。
所以从两个的定义来看，给定整个goal序列，那么某个时刻t，处于某一个状态的概率的大小就等价于前后向信息的乘积（从1到达t，以及从t到达T的概率乘积）

11.3 Together with soft optimality

有了soft optimality，就可以把之前的经典算法（比如Q-learning，policy gradient等等）中的max，用soft max替换；greedy policy用soft policy替换，这样更有利于做exploration，允许次优的动作，更加鲁棒等等的好处。

11.3.1 Q-learning with soft optimality

Q-learning是一个model-free off-policy的方法，他通过直接最大化Q来贪心的优化policy。这里off-policy是指采样数据不是来自policy本身，而是来自$\max_{a} Q(s,a)$。假设我们仍然采用function approximation，并且和target之间的loss选择L2，那么Q-learning的更新式子为：

\[\phi \leftarrow \phi + \alpha \triangledown_\phi Q_\phi(s,a) \left( r(s,a) + \gamma V(s')- Q_\phi(s,a) \right)\]

其中，Q-target中$V(s’)=\max_{a} Q_\phi(s’,a’)$。现在把他用soft max替换（这里略去了那个uniform项），随之policy也改为soft的

\[V(s')=\log \int \exp(Q_\phi(s',a'))da'\\ \pi(a\mid s)=\exp(A(s,a))\]

算法的伪代码可以用下面表示：

11.3.2 Policy gradent with soft optimality

从理论上来说：当policy gradient的policy采用$\pi(a\mid s)=\exp(A(s,a))$，那么等价于最大化下式。这个式子相比于之前的方法，多了一项policy entropy $H(\pi(a\mid s_{t}))=E_{\pi(a_{t}\mid s_{t})}[-\log \pi(a_{t}\mid s_{t})]$。相当于是加了一个最大熵的正则

\[\max \sum_t E_{\pi(s_t,a_t)} [r(s_t,a_t)] + E_{\pi(s_t)}[H(\pi(a_t\mid s_t))]=\sum_t E_{\pi(s_t,a_t)}[r(s_t,a_t)-\log \pi(a_t\mid s_t)]\]

第二项起到了一个最大熵模型的作用，整个式子就是最大化累计reward的同时，policy的熵最大。保证那些能最大化return的policy都有可能被选中。往深入来说，加入soft optimality之后的policy gradient和Q-learning是有联系的：

\[\mbox{Soft policy gradient: }\frac{1}{N}\sum_t\sum_t\left( \triangledown_\theta Q(a_t\mid s_t) - \triangledown_\theta V(s_t)\right) \left( r(s_t,a_t) + Q(s_{t+1},a_{t+1})-Q(s_t,a_t)) \right)\\ \mbox{Soft Q-learning: }-\frac{1}{N}\sum_t\sum_t \triangledown_\theta Q(a_t\mid s_t) \left( r(s_t,a_t) + soft max Q(s_{t+1},a_{t+1})-Q(s_t,a_t)) \right)\\\]

policy gradient是在advanced function的基础上的gradient ascent，Q-learning是在Q函数的基础上的gradient descent
Q-learning的off-policy体现在soft max上。这里也可以使用on-policy的sarsa，这时候就没有soft max了，而是和policy gradent中的那一项一样

12. Inverse Reinforcement Learning

在model-based RL章节里，提到过用table lookup的方法来学习reward function，但是所学到的模型的泛化能力依赖于训练数据。实际上在现实的问题中，dynamics是不一定能提供reward的，比如在部分游戏中，可能会有score broad来提供reward，但是还有很多应用下，是没办法由dynamics给出reward function的。这种情况下，一般是由专家知识给定，但是太浪费人力了，也太依赖专业知识了。所以，缺失reward的问题限制了很多RL的应用场景。

那么，reward能不能通过学习出来？这个问题就是inverse RL 要解决的。IRL是想学习出一个reward function，并且再用它来学习一个policy。IRL对于reward的学习策略的核心思想，在于以专家（expert）为模子，通过expert的行为去推测task是什么，从而学习reward function应该怎么设置（才能让expert的return最大）。比如在下面这个gif里，研究人员试图去捡起地上的东西，但是够不着，旁边的小朋友推测出研究人员的意图之后，主动的帮忙捡了起来。在这个例子里，捡东西这个动作就应该被赋予更大的reward。

当然，对expert意图的推测，一方面，问题本身是很难的。如果我观察到expert把下图的圆推到了右边，但是expert是出于喜欢蓝色，讨厌红色的原因才这么做？还是说有风吹向右边，所以export顺风推到了右边？另一方面，expert的动作不一样是最优的（Soft oplimality）。

形式化来说，IRL是在给定state& action space和expert 行为样本，（以及 transition dynamics）的条件下，去学习一个reward function，并用这个reward function来进一步学习policy。这里的reward function可以自己定义他的形式，比如比较常用的linear reward function $r_\psi(s,a)=\psi^Tf(s,a)$，其中$f(s,a)$表示根据state和action提取到的特征向量，$\psi$表示reward function的参数。当然也可以使用deep network来学习reward

IRL的目标就可以表示为，$\pi^\star \approx \pi^{r_{\psi}}$。也就说，要找一个reward function r，使得r下的最优policy $\pi^{r_\psi}$要尽可能的贴近在真实reward function下的最优策略$\pi^\star$。那么，下面朝着这个目标，我们来介绍一些IRL的算法

12.1 Feature matching based IRL

IRL的目标$\pi^\star \approx \pi^{r_{\psi}}$是很难直接刻画的，但是，如果两个policy一样，那么在相同的dynamics下，他们走出来的episode就应该很相似。Feature Matching就是从这个角度出发，它意思就说，要找一个参数$\psi$使得episode的特征的期望是相等的，即下式成立

\[E_{\pi^{r_\psi}}[f(s,a)]=E_{\pi^\star}[f(s,a)]\]

但是，反过来看，满足上面等式的$\psi$，不一定能使得policy是相似的。他可能会存在很多解，这些解都能match feature，但是policy会很不一样。这时候，大牛们就用了SVM的类似方法，在从多的解中选择一个能最大化margin的解，并且还要保证policy的相似性：

\[\min \frac{1}{2} \mid \mid \psi \mid \mid^2\\ \mbox{s.t. } \psi^TE_{\pi^\star}[f(s,a)] \geq \max_{\pi} \psi^TE_{\pi}[f(s,a)] + D(\pi, \pi^\star)\]

上面式子的约束条件整体是一个adaptive margin的样子，松弛变量是D，它刻画了policy之间的差异。然后在原始feature match的基础上，还与$\psi$做了内积，表示一个average reward。所以，约束表示保证policy相似的情况下，reward尽可能的与真实值接近。问题就是，这个解确实不好求。而且，最大间隔这个假设对不对还是挺arbitrary。

12.2 MaxEnt IRL

考虑到expert的动作可能不是最优的，那么就可以借用上一章的soft optimality的方法，把PGM inference和学习reward function相结合（如下式）。这时候PGM中的goal不在是已知的了，而是需要去学习的，但是我们拥有一些expert的episode数据，所以s,a是已知的。

\[P(\tau \mid O_{1:T}) \propto P(\tau) \exp\left( \sum_t r_\psi(s_t,a_t) \right)\]

那么问题就转化为PGM中的参数学习，只需要最大化likelihood $\log P(\tau \mid O_{1:T}, \psi)$就可以了。这里我们把$P(\tau)$给省略了，因为它和参数无关，所以$P(\tau \mid O_{1:T}, \psi)$只需要简单的归一化，其中$Z$是normalizer。

\[P(\tau \mid O_{1:T}, \psi)=\frac{P(\tau \mid O_{1:T}, \psi)}{\int P(\tau \mid O_{1:T}, \psi) d\tau}=\frac{P(\tau \mid O_{1:T}, \psi)}{Z}\\ \max_\psi \frac{1}{N} \sum_{i=1}^N \log P(\tau_i \mid O_{1:T}, \psi)=\frac{1}{N} \sum_{i=1}^N r_\psi(\tau_i) - \log Z\]

咋一看，上面式子里的Z，就和PGM中MRF中的normalizer一样的讨厌，因为它对参数的导数不好求。但是在这里是个特例，他可以化解成一个简洁的形式。当对上式求导的时候，有下式成立（注意$P(\tau \mid O_{1:T}) = P(\tau) \exp\left( \sum_{t} r_\psi(s_{t},a_{t}) \right) / Z$）

\[\triangledown_\psi L= \frac{1}{N}\sum_{t=1}^N \triangledown_\psi r_\psi(\tau_i) - \frac{1}{Z} \int P(\tau) \exp(r_\psi(\tau)) \triangledown_\psi r_\psi(\tau) d\tau\\ =E_{\tau \sim \pi^\star(\tau)} [\triangledown_\psi r_\psi(\tau)] - E_{\tau \sim P(\tau \mid O_{1:T}, \psi)}[\triangledown_\psi r_\psi(\tau)]\]

上面的式子的第一项是expert的episode下的期望，第二项是当前reward下的soft policy下的采样episode下的期望。那么，我们就可以通过采样的方式来计算出导数。对于第二项来说：由于期望和求和都是线性的，那么可以交换他们的次序：

\[E_{\tau \sim P(\tau \mid O_{1:T}, \psi)}[\triangledown_\psi r_\psi(\tau)]= \sum_{t=1}^T E_{(s_t,a_t)\sim P(s_t,a_t \mid O_{1:T}, \psi) }[\triangledown_\psi r_\psi(s_t,a_t)]\]

为了计算上面的式子，首先需要求得state和action的后验概率$P(s_{t} ,a_{t} \mid O_{1:T}, \psi)$。这里可以使用贝叶斯公式：

\[P(s_t,a_t \mid O_{1:T}, \psi)=P(a_t\mid s_t,O_{1:T}, \psi) P(s_{t}\mid O_{1:T}, \psi)\]

等式右边的第一项就是上一章中的policy，第二项就是上一章做的inference

\[P(a_t\mid s_t,O_{1:T}, \psi) = \frac{\beta(s_t,a_t)}{\beta(s_t)}\\ P(s_{t}\mid O_{1:T}, \psi) \propto \beta(s_t) \alpha(s_t)\\ P(s_t,a_t \mid O_{1:T}, \psi) \propto \beta(s_t,a_t)\alpha(s_t)\]

计算得到$P(s_{t} ,a_{t} \mid O_{1:T}, \psi)$之后，就可以得到导数了。这个计算过程就是MaxEnt算法。下面是他的伪代码（这里有个变量替换$\mu(s_{t}, a_{t}) = P(s_{t} ,a_{t} \mid O_{1:T}, \psi)$）

这个算法和feature matching有一定的联系。在理论上，MaxEnt算法等价的优化目标是：

\[\max_\psi H(\pi^{r_\psi}) \\ \mbox{s.t. }E_{\pi^{r_\psi}}[f(s,a)]=E_{\pi^\star}[f(s,a)]\]

这个是个标准的最大熵模型（H是熵，所以叫MaxEnt算法）。他不在有最大间隔的假设，而是在满足feature matching的条件下，尽量保证学到的policy的随机性。当然，这个方法计算量太大了，根本处理不了large MDPs，并且我们需要知道transition dynamics才能计算forword和backward message 。

12.3 Sampling-based MaxEnt IRL

我们的目标是适应large MDP和连续state和action空间，以及在unknown dynamics的情况下能使用IRL。或许，一方面可以走model-based 的方法，把transition dynamics给学习出来，比如lookup table，但是累计损失会更可怕（学习transition，再学习reward，最后学policy）；另一方面直接用model-free的方法，不知道transition，但是我们可以得到episode samples。

在MaxEnt中，只有求导数的时候用到了dynamics，如果可以拿到当前的policy $P(a_{t} \mid s_{t}, O_{1:T}, \psi)$，然后用这个policy sample出一些样本，那么，我们仍然是可以求得到导数的。这时候我们就需要使用expert的episode来计算第一项，用current policy samples来计算第二项

\[\triangledown_\psi L=E_{\tau \sim \pi^\star(\tau)} [\triangledown_\psi r_\psi(\tau)] - E_{\tau \sim P(\tau \mid O_{1:T}, \psi)}[\triangledown_\psi r_\psi(\tau)]\\ \approx \frac{1}{N} \sum^N_{t=1} \triangledown_\psi r_\psi(\tau_i) - \frac{1}{M} \sum^M_{j=1} \triangledown_\psi r_\psi(\tau_j)\]

然而，问题在于policy的学习依赖reward。所以直接学出policy是很难的。另一种思路就是，仿照policy iteration或者value iteration一样，我们去improve current policy，而不是一次性学习到。但是这样做又会引入新的问题：样本来自一个非optimal的policy，这样计算得到的结果是有偏的。一个解决策略就是使用importance sampling（IS）！

\[\triangledown_\psi L \approx \frac{1}{N} \sum^N_{t=1} \triangledown_\psi r_\psi(\tau_i) - \frac{1}{\sum_j w_j} \sum^M_{j=1} w_j \triangledown_\psi r_\psi(\tau_j)\\ w_j = \frac{\pi^{r_\psi}(\tau_j)}{\pi^{IS}(\tau_j)}=\frac{P(\tau \mid O_{1:T})}{P^{IS}(\tau)}=\frac{P(s_1)\prod_t P(s_{t+1}\mid s_t)P(a_t\mid s_t)\exp(r_\psi(s_t,a_t))}{P(s_1)\prod_t P(s_{t+1}\mid s_t)\pi(a_t\mid s_t)}\\ =\frac{\prod_t P(a_t\mid s_t)\exp(r_\psi(s_t,a_t))}{\prod_t \pi(a_t\mid s_t)}\]

这里还是假设$P(a_{t}\mid s_{t})$是uniform的，取一个定值，所以$w_{j}=\prod_{t} \frac{ \exp(r_\psi(s_{t},a_{t}))}{ \pi(a_{t}\mid s_{t})}$。所以现在可以用importance sampling的新的policy $\pi$下进行采样，再加权，用于计算导数。这样随着迭代的进行，reward的参数渐渐学习到，也渐渐的逼近optimial policy。这就是guided cost learning的大致算法框架：输入IS的$\pi$和expert数据，通过policy的来更新reward，reward也用来更新policy。

他可以在unknown transition的背景下，可以采用function approxiation的方式来近似reward与$\pi$，以处理large/continuous MDPs。

12.4 GAN & IRL

最后来看一下IRL和GAN的联系。根据一些文献的结果显示，IRL中引入的policy起到了GAN中generator的作用，而reward则是disciminator。reward要区别出expert的数据和policy生成的数据。

[NIPS’16] Generative Adversarial Imitation Learning

[ICML’17] Use learned dynamics model to backdrop through discriminator

13. Advanced Policy Gradient

我们在一开始讲了policy gradient，它想找一个policy以最大化累计reward。结合convenient identity，这个问题可以通过梯度的方法迭代求解

\[\theta^*=\arg\max_\theta E_{\tau \sim \pi_\theta(\tau)} \left[ \sum_{t=1} \gamma^{t-1} r(s_t,a_t) \right]\\ \bigtriangledown_\theta J(\theta)=E_{\tau \sim \pi_\theta(\tau)} \left[ \left(\sum_{t=1}^T \bigtriangledown_\theta log \pi_\theta(a_t\mid s_t) \right) \left( \sum_{t=1}^T \gamma^{t-1} r(s_t,a_t)\right) \right]\]

甚至还可以考虑Actor-critic和reward to go的策略，通过下式求梯度，以减小方差

\[\bigtriangledown_\theta J(\theta)=E_{\tau \sim \pi_\theta(\tau)} \left[ \sum_{t=1}^T \gamma^t \bigtriangledown_\theta log \pi_\theta(a_t\mid s_t) A^{\pi_\theta}(s_t,a_t) \right]\]

但是这种方法仍然有一些问题：

poor sample efficiency：policy gradient通常是on-policy的，每次gradient update之后，policy就变了。也就需要重新采样数据，之前的数据必须丢弃。虽然，可以考虑用importance sampling变成off-policy policy gradient：
\[\bigtriangledown_\theta J(\theta) = E_{\tau \sim \pi'(\tau)} \left[\frac{\pi_\theta(\tau)}{\pi'(\tau)} \bigtriangledown_\theta log \pi_\theta(\tau) r(\tau)\right]\]
但是Importance sampling的策略还是有两个bugs，第一，IS来带的方差是很大的！从图上来看，如果使用target是P，IS用Q来采样的话，在Q和P的相似性不高的时候，Q会采样出很多几乎无效的样本（他们的权重很小，图中的bar表示权重）。而且很难选中一个和P相似的Q。

从数学上来说：IS做的核心就是下式：
\[E_{x \sim P} [ f(x)] = E_{x \sim Q}\left[ \frac{P(x)}{Q(x)}f(x) \right]\]
但是，它的方差就很恐怖了
\[Var\left(\frac{P(x)}{Q(x)}f(x)\right)=E_{x \sim Q} \left[ (\frac{P(x)}{Q(x)}f(x))^2 \right] - E_{x \sim Q} \left[ \frac{P(x)}{Q(x)}f(x) \right]^2\\ = \int Q(x) (\frac{P(x)}{Q(x)}f(x))^2 dx - (\int \frac{P(x)}{Q(x)}f(x) Q(x) dx)^2\\ =E_{x \sim P}\left[ \frac{P(x)}{Q(x)}f(x)^2 \right] - E_{x \sim P}\left[ f(x) \right]^2\]
可以看到，一旦$\frac{P(x)}{Q(x)}$变大，那么这个方差是很大的。另外，IS的第二个bug在于Exploding or vanishing importance sampling weights。当使用IS的时候，policy gradient可以写成下式：
\[\bigtriangledown_\theta J(\theta) =E_{\tau \sim \pi'(\tau)} \left[ \sum_{t=1}^T \bigtriangledown_\theta log \pi_\theta(a_{i,t}\mid s_{i,t}) \left(\prod_{t'=1}^t \frac{\pi_\theta(a_t'\mid s_t')}{\pi'(a_t'\mid s_t')}\right) \left( \sum_{t‘=t}^T \gamma^{t'-t} r(s_{i,t'},a_{i,t'})\right)\right]\]
问题就出在式子中的叠乘项。即使如果一条episode中，每个时刻Q和P只有一点点不一样，但是他们叠乘起来，这个数就会变得很畸形了。更不要说还可能是多个小于1的数叠乘会引发weights vanishing，多个大于1的数叠乘会引发weight exploding。总的来说，求解效果会很不稳定。
gradient的更新步长很难确定，这个问题算是老生常谈了。步长太大，会跨过最优点，甚至会在最优点附近震荡。步长太小的话，收敛速度就会很慢
参数空间不等于policy 空间。感觉这算是一个收敛敏感性的问题。比如下图参数$\theta$发生等距的变化（从4, 再到2, 最后到0）但是在policy的变化却可能会很大。policy空间可能参数敏感的，在这种情况的优化policy，会很困难。

另一个例子是下图。当均值都从-1变到1的时候，很明显第一个图中的Gaussian变化更大。所以，不同的参数对分布的影响是不同的（比如均值和方差），传统的梯度下降是将每个参数的影响都视为一样的，因此，我们需要将参数对整体输出的影响考虑进去，并且根据它来scale每一个参数。

为了处理以上的问题，大牛们提出了很多高级的算法。本章就这些算法做一个总结。

13.1 Policy performance bounds

原policy gradient的方法的目标是最大化累计reward，

\[J(\pi_\theta)=E_{\tau \sim \pi_\theta(\tau)} \left[ \sum_{t=1} \gamma^{t-1} r(s_t,a_t) \right]\]

这种方式不可避免的会有上面所提到的问题。大牛们转而去优化另一个目标：与其直接最大化，不如刻画一个相对的关系。这种相对关系建立在relative policy performance identity之上。所谓的relative policy performance identity是指，对于任意两个policy，一定满足下面的关系。下面等式的左边刻画两个policy在累计reward方面的差异

\[J(\pi')-J(\pi)=E_{\tau \sim \pi'} \left[ \sum_{t=0} \gamma^t A^\pi(s_{t},a_{t})\right]\]

这个等式成立的原因在于下式。其中因为episode已经得到了，所以第二行中是$V(s_{t+1})$而不是$V(S_{t+1})$。倒数第二行到最后一行是通过展开后抵消得到的。最后一行中$E_{\tau \sim \pi’}[V^\pi(s_{0})]$，由于只依赖了$\pi’$的episode的初始状态，后面的trajectory都是通过$\pi$来走的，所以他就是$J(\pi)$。

\[J(\pi')-J(\pi)=E_{\tau \sim \pi'} \left[ \sum_{t=0} \gamma^t A^\pi(s_{t},a_{t})\right]\\ =E_{\tau \sim \pi'} \left[ \sum_{t=0} \gamma^t (r(s_t,a_t)+\gamma V^\pi(s_{t+1}) - V^\pi(s_t))\right]\\ =J(\pi') + E_{\tau \sim \pi'} \left[ \sum_{t=0} \gamma^{t+1} V^\pi(s_{t+1}) - \sum_{t=0} \gamma^t V^\pi(s_t)\right]\\ =J(\pi') + E_{\tau \sim \pi'} \left[ \sum_{t=1} \gamma^{t} V^\pi(s_{t+1}) - \sum_{t=0} \gamma^t V^\pi(s_t)\right]\\ =J(\pi') + E_{\tau \sim \pi'}[V^\pi(s_0)] =J(\pi')-J(\pi)\]

如果$\pi’=\pi^{(k+1)},\pi=\pi^{(k)}$，那么relative policy performance identity就提供了一个不断迭代提上policy的方法，我们只需要最大化下式。但是，bug是我们需要从$\pi’$中进行采样才能计算后面的期望。

\[\pi^{(k+1)}=\arg\max_{\pi'} J(\pi')-J(\pi^{(k)})=E_{\tau \sim \pi'} \left[ \sum_{t=0} \gamma^t A^{\pi^{(k)}}(s_{t},a_{t})\right]\]

我们得到episode，也就希望能采样得到$(s_{t},a_{t})$的序列。假设state来自一个于policy和dynamics共同作用的分布$d$（transition dynamics需要结合policy的action，才能确定下一时刻的state），那么接下来的action自然而然来源于policy。一般来说这里的分布$d$选为 discounted future state distribution $d^\pi$：

\[d^\pi(s)=(1-\gamma) \sum_{t=0}^\infty \gamma^t P(s_t=s \mid \pi)\]

这个分布的定义方式和$TD(\lambda)$中的$\lambda$-return如出一辙。$d^\pi$刻画了访问state s的频率，但是随着时间的进行，每次访问的权重成指数衰减。这时候，relative policy performance identity就可以写成下式。其中，第三行是采用了importance sampling，第四行为了方便计算，采用$d^\pi$近似了$d^{\pi’}$，并且这种近似方法是有理论保证的。

\[J(\pi')-J(\pi)=E_{\tau \sim \pi'} \left[ \sum_{t=0} \gamma^t A^\pi(s_{t},a_{t})\right]\\ =\sum_{t=0} \sum_{s}\gamma^t P(s_t=s\mid \pi') \sum_{a} \pi'(a\mid s) A^\pi(s_{t},a_{t})\\ =\frac{1}{1-\gamma} E_{s \sim d^{\pi'}, a \sim \pi'} [A^\pi(s,a)] \\ =\frac{1}{1-\gamma} E_{s \sim d^{\pi'}, a \sim \pi} [ \frac{\pi'(a \mid s)}{\pi(a\mid s)} A^\pi(s,a)]\\ \approx \frac{1}{1-\gamma} E_{s \sim d^{\pi}, a \sim \pi} [ \frac{\pi'(a \mid s)}{\pi(a\mid s)} A^\pi(s,a)] = L_\pi(\pi')\\ =E_{\tau \sim \pi} \left[ \sum_{t=0} \gamma^t \frac{\pi'(a_t \mid s_t)}{\pi(a_t\mid s_t)} A^\pi(s_t,a_t) \right]\]

所以目标转移成最大化$L_\pi(\pi’)$，并且这时候我们只需要对当前已知的policy采样来计算这个期望项。同时也避免了Exploding or vanishing importance sampling weights，因为这里的weights仅仅与当前时刻有关。理论上来说，这个近似方法同时也是有bound的，这就是relative policy performance bounds。这个bound说明，在$\pi$和$\pi’$很接近的时候，近似误差是很小的。

\[\mid J(\pi')-(J(\pi)+L_\pi(\pi')) \mid \leq C \sqrt{E_{s \sim d^\pi}[D_{KL}(\pi' \mid \mid \pi)[s]]}\\ D_{KL}(\pi' \mid \mid \pi)[s]=\sum_{a} \pi'(a\mid s)\log \frac{\pi'(a\mid s)}{\pi(a\mid s)}\]

更有趣的是，$L_\pi(\pi’)$对policy $\pi’$的参数$\theta$的导数在$\theta_{k}$处的取值正好就是policy gradient，这里记当前policy为$\pi_{\theta_{k}}$：

\[\triangledown_\theta L_{\theta_k}(\theta) \mid_{\theta_k} = E_{\tau \sim \pi_{\theta_k}} \left[ \sum_{t=0} \gamma^t \frac{\triangledown_\theta \pi_\theta(a_t \mid s_t) \mid _{\theta_k}}{\pi_{\theta_k}(a_t \mid s_t)} A^{\pi_{\theta_k}}(s_t,a_t) \right] \\ =E_{\tau \sim \pi_{\theta_k}} \left[ \sum_{t=0} \gamma^t \triangledown_\theta\log \pi_\theta(a_t\mid s_t) \mid_{\theta_k} A^{\pi_{\theta_k}}(s_t,a_t) \right]\]

13.2 Monotonic Improvement Theory

根据performance bound显示，上文直接最大化$L_\pi(\pi’)$，是不一定能保证policy improvement。因为他还与KL散度有关。所以正确的姿势应该是最大化下式：

\[\pi^{(k+1)}=\arg\max_{\pi'} L_{\pi^{(k)}}(\pi' )- C \sqrt{E_{s \sim d^{\pi^{(k)}}}[D_{KL}(\pi' \mid \mid \pi^{(k)})[s]]}\\ \mbox{因为：} J(\pi') - J(\pi) \geq L_\pi(\pi') - C\sqrt{E_{s \sim d^{\pi^{(k)}}}[D_{KL}(\pi' \mid \mid \pi^{(k)})[s]]}\]

这个目标都可以从当前的policy中进行采样来估计，并且这个方法是一定能提升policy的。因为当$\pi’=\pi^{(k)}$的时候，KL散度那一项一定是等于0 的，$E_{\tau \sim \pi} \left[ \sum_{t=0} \gamma^t A^\pi(s_{t},a_{t}) \right]$也一定是等于0 的。所以当优化目标被最大化的时候，至少也是0了。也就说，最优值大于等于0，$J(\pi’)-J(\pi) \geq 最优值$。所以policy一定是提升的。

在实际使用中，参数$C$就很影响了，如果C太大，就要求policy一尘不动，这样就相对于SGD中的步长太小，收敛太慢。理论上的C值满足$C \propto (\frac{1}{1-\gamma})^2$，所以当$\gamma$接近1的时候，这个优化步长就相当小了。所以大牛们把原问题改成约束优化问题：

\[\pi^{(k+1)}=\arg\max_{\pi'} L_{\pi^{(k)}}(\pi' )\\ \mbox{s.t. }E_{s \sim d^{\pi^{(k)}}}[D_{KL}(\pi' \mid \mid \pi^{(k)})[s]] \leq \delta\]

这种转换能保证KL散度的误差在一定范围内，这个范围叫做信赖域（trust region），并且大佬们证明这个方式也能保证在 worst case下有所提升。这个优化问题就是后面要介绍的算法的理论基础。它使用当前的policy来采样，以计算L和E，从而得到improved policy；并且这里是直接优化的policy $\pi$，这就和policy的参数空间的畸形与否，关系不大了。

13.3 Advanced Policy Gradient Algorithms

13.3.1 Natural Policy Gradient (NPG)

NPG主要是为了处理parameters space和policy space的in-covariant而提出的。他最后的下降方向是$H^{-1}g$，其中$g$是梯度，$H$是一个Fisher Information matrix。NPG通过使用H来scale parameter，达到covariant 的目的（也就是前文提到的PG的第三个问题）。当$H=I$的时候，NPG就是普通的PG下降方向了。

给定参数$\theta$和数据$X$下的似然函数$L(X;\theta )$，Fisher Information Matrix 定义为Score function的二阶矩 $E[S(X;\theta)^2]$。其中score function $S(X; \theta) $是 $\log L(X;\theta)$对参数$\theta$的一阶导。

Under specific regularity conditions，fisher information刻画了最大似然估计的方差，等同于log 似然的负二阶导数的期望 $-E[\frac{\partial^2 \log L(X;\theta)}{\partial \theta^2}]$.。Fisher Information反映了我们对参数估计的准确度，它越大，对参数估计的准确度越高，即代表了越多的信息。

NPG优化细节是通过用泰勒展开来近似原始目标方程。

\[\max_{\pi'} L_{\pi^{(k)}}(\pi' )\\ \mbox{s.t. }D_{KL}(\pi' \mid \mid \pi^{(k)})\leq \delta\]

其中L被近似到一阶，KL被近似到二阶，两者都是在$\theta=\theta_{k}$的地方进行展开（$\theta$是policy的参数），下面把他们写成参数的形式进行近似：

\[L_{\theta_k}(\theta) \approx L_{\theta_k}(\theta_k) + g^T (\theta - \theta_k) , \mbox{ } g=\triangledown_\theta L_{\theta_k}(\theta) \mid_{\theta_k}\\ D_{KL}(\theta \mid \mid \theta_k) \approx \frac{1}{2} (\theta-\theta_k)^T H (\theta-\theta_k), \mbox{ } H= \triangledown^2_\theta D_{KL}(\theta \mid \mid \theta_k)\mid_{\theta_k}\]

注意，对于KL散度来说，原始的近似是长这样的：

\[D_{KL}(\theta \mid \mid \theta_k) \approx D_{KL}(\theta_k \mid \mid \theta_k) + g_{KL}^T (\theta-\theta_k)+ \frac{1}{2} (\theta-\theta_k)^T H (\theta-\theta_k)\]

对于右端的第一项显然为0，对于第二项，他其实也是为0的：

\[D_{KL}(\theta \mid \mid \theta_k) = \int \pi_\theta(s) \frac{\log \pi_\theta(s)}{\log \pi_{\theta_k}(s)} ds\\ \triangledown_\theta D_{KL}(\theta \mid \mid \theta_k) = \int \triangledown [ \pi_\theta(s) \log \pi_\theta(s)] ds - \int \triangledown \pi_\theta(s) \log \pi_{\theta_k}(s) ds\\ = \int \triangledown \pi_\theta(s)(1+\log \pi_\theta(s) ) ds - \int \triangledown \pi_\theta(s) \log \pi_{\theta_k}(s) ds\\ = \int \triangledown \pi_\theta(s)(1+\log \pi_\theta(s) - \log \pi_{\theta_k}(s) )ds \\ = \int \triangledown \pi_\theta(s)(\log \pi_\theta(s) - \log \pi_{\theta_k}(s) )ds\\ \mbox{因此：}g_{KL}^T=\triangledown_\theta D_{KL}(\theta \mid \mid \theta_k)\mid_{\theta_k} =0\]

式子中，那个1的去掉方法是这个：

\[\int \triangledown \pi_\theta(s) ds = \triangledown \int \pi_\theta(s) ds = \triangledown 1 = 0\]

所以，对于NPG来说，他的优化目标变成了下面的样子：

\[\theta_{k+1} = \arg \max_\theta g^T (\theta - \theta_k) \\ \mbox{s.t. } \frac{1}{2} (\theta - \theta_k)^T H (\theta - \theta_k) \leq \delta\]

这个是个QCQP问题，可以用KKT来解他。先写出他的拉格朗日式子（原始优化是求的max，注意加个负号让他变成min）

\[L= g^T (\theta_k - \theta) - \lambda \left( \frac{1}{2} (\theta - \theta_k)^T H (\theta - \theta_k) - \delta \right)\]

我们可以得到他的KKT条件（实际上根据前两条件就可以求解了）：

stationarity condition: $\frac{\partial L}{\partial \theta}=0 \rightarrow \theta=\theta_{k}+\frac{1}{\lambda} H^{-1}g$
complementary condition: $\lambda \left( \frac{1}{2} (\theta - \theta_{k})^T H (\theta - \theta_{k}) - \delta \right)=0$
primal & dual feasibility: 略

由于不等式约束的拉格朗日变量$\lambda>0$，所以得到：

\[\left\{\begin{matrix} \theta=\theta_{k}+\frac{1}{\lambda} H^{-1}g \\ (\theta - \theta_{k})^T H (\theta - \theta_{k}) = 2\delta \end{matrix}\right.\]

我们可以把第一项导入到第二项中，求出$\lambda$，然后得到NPG的最后更新公式：

\[\theta=\theta_{k}+ \sqrt{\frac{2\delta}{g^TH^{-1}g}} H^{-1}g\]

最后NPG的伪代码为下图。另外NPG要计算一个H的逆，这个复杂度很高很高。这个问题有其他的改进策略，比如Truncated NPG。

13.3.2 Trust Region Policy Optimization (TRPO)

NPG算法很厉害，但是在实际使用中有两个问题：

$\delta$的选择
泰勒展开近似KL散度的时候，原始约束可能会被破坏，不准确。

这两个问题都可以通过步长选择的方式来避免。这里步长是$s=\sqrt{\frac{2\delta}{g^TH^{-1}g}}$。如果步长太大，导致不满足原始约束( $D_{KL}(\theta \mid \mid \theta_{k}) > \delta $)，或者保证不了policy improvement ($L_{\theta_{k}}(\theta) < 0$)，那么就缩小步长。步长成指数衰减，衰减因子为$\alpha\in (0,1)$。伪代码如下：

在上面的算法中，结合这个步长方法就是TRPO了。图中箭头标注的部分是用来计算$H$的逆矩阵的，类似于Truncated NPG的策略，采用Conjugate Gradient (CG) 算法。

下图给出了很多算法的效果，y轴是平均reward。其中Truncated NPG和TRPO算法的性能确实是最好的，不仅score高，方程还小

13.3.3 Proximal Policy Optimization (PPO)

PPO算法可以进一步的优化计算量，PPO并不会去计算natural gradient，所以不会去计算$H^{-1}$。他会直接去计算一个带有截断效应的代理函数(clipped surrogate function)。虽然PPO没有啥理论依据，但是他的效果是很好的。PPO有两种实现：

Adaptive KL：他把原始的无约束优化问题中的$C$，变成了一个与迭代次数有关的书$\beta_{k}$。每次迭代会修正这个值

\[\max_{\pi'} L_{\pi^{(k)}}(\pi' ) + \beta_k D_{KL}(\pi' \mid \mid \pi^{(k)})\]

Clipped function：这时候的优化方程也是无约束的，用截断函数clip来替换了，$clip(A,B,C)$是说，如果A超过了最小值B，则等于B；超过最大值C，就取C，否则取A。另外$r_{t}(\theta)=\frac{\pi_\theta(a_{t} \mid s_{t})}{\pi_{\theta_{k}}(a_{t}\mid s_{t})}$，通常$\epsilon=0.2$
\[\max_{\theta} L_{\theta_{k}} ^{Clip}(\theta)=E_{\tau \sim \pi_k} \left[\sum_{t=0}^T[\min(r_t(\theta)A_t^{\pi_k}, clip(r_t(\theta), 1-\epsilon, 1+\epsilon)A_t^{\pi_k})] \right]\\ \theta_{k+1} = \arg\max_{\theta} L_{\theta_{k}} ^{Clip}(\theta)\]

对于第一个算法，他的伪代码如下：

第二种：

14. Exploration and Exploitation

RL其中一个bug就在于搜索空间太大，难以找到全局最优解。这个问题可以等同于是探索（exploration）和利用（exploitation）之间的矛盾：到底是要根据已有的信息，做出决策；还是去探索未知，收集更多信息。探索未知，可能得不到一个好的（long-term或者short-term）reward，但是不去做，又没法知道。就好比，如果做action a1，可能得到10份，但是action a2的不确定性很高，它可能会带来5分到20分之间的一个reward，那么去不去做a2呢？这要求我们有一个好的探索策略，知道什么时候该去explore，什么时候该去exploit。

在之前的几个章节里，多多少少已经用到了exploration。比如$\epsilon-$greedy，MCTS，甚至off-policy的思想也有一点点exploration的意思（用其他不准确的policy来采样动作，有引入噪声和扰动，起到一点点exploration的效果）。这个问题发展至今，有很多的算法被相继提出，包括：

Naive/Greedy Exploration
Upper Confidence Bound
Posterior Sampling / Probability Matching
Information State Search
Information Gain based

这些方法或多或少都是建立在multi-armed bandits问题之上。首先来看这个基础

14.1 Multi-Armed Bandits

Bandits问题就是有一台赌博机，每次pull arm的时候，他会给一个reward。Multi-Armed Bandits就是有多台这样的赌博机，每一台有一定的概率$P(r\mid a_{i})$给一个reward，但是玩家并不知道任何一台赌博机出现reward大小的概率分布，玩家需要每次选择一个机器，然后pull arm，得到reward

这个网页是一个类似的游戏。你需要在多种药中，每次选择一种，给病人服用。病人可能会治愈，可能会死亡。你需要根据病人的反馈，决定下一次要不要给下一个病人换药。当然，你的目的在于让更多的病人被治愈。

Multi-armed bandits可以看做是一个特殊的MDP，他没有状态空间，并且action space有m个动作，对应m个bandits。第$t$时刻，动作$a_{t}$表示去拉某一个机器的arm，每次动作之后会有一个反馈$r_{t}=R^{a_{t}}$。所以，我们的目标是最大化累计reward $\sum_{t}r_{t}$。这里没有discount，是因为Multi-armed bandits的episode长度为1，即，拉完一个arm之后，这个episode就结束了。

如果，一开始就知道每台机器的详细情况，出现大值reward的概率等等（这在实际情况中是很不现实的），那么就可以每次都做出一个最优的动作$a^\star$。因此，它对应的最优V函数表示为下式（注意，由于bandits问题是一个没有状态的MDP，所有Q函数里把state给删掉了）

\[V^\star = Q(a^\star)=\max_{a} Q(a)\\ Q(a)=E[r\mid a]\]

我们要做的，就是尽可能的去达到最优值，减小我们的策略与最优之间，所得到reward的差异，这个差异称为regret，它表示后悔没有选最优的动作。（Multi-armed bandits实际上是online learning中的一个分支，online learning要做的事也是最小化total regret）

\[Regret=E\left[ \sum_{\tau}^t V^\star - Q(a_\tau)\right]\]

对于Multi-armed bandits问题来说，这个regret的形式可以进一步的简化。令$N_{t}(a)$表示选中动作a的次数，$\triangle_{a}=V^\star-Q(a)$表示动作a与最优动作之间的差距，那么，regret可以简化成下式。

\[Regret=E\left[ \sum_{\tau}^t V^\star - Q(a_\tau)\right]=\sum_a E[N_t(a)]\triangle_a\]

这个式子的含义在于：最小化regret就是要减少那种效果很差的动作的发生次数。我们希望的效果，随着pull arm的次数增加，我们能掌握更多信息，犯错的次数越来越少（如图中的黑线，随着实验次数增加，regret的总量有了上界），我们不能接受的是一直在犯错（图中蓝线和红线）。不幸的是，在不知道$V^\star$的情况下，还没有算法能达到黑线的效果，我们只能不断的接近黑线，让regret有一个稍差一些的上界。这个上界一般称为Regret bound，它是衡量online learning method的一个很重要的指标。（图中的黑线代表的bound是sublinear的）

Multi-armed bandits作为很多问题的基础，是因为它具有很好的理论基础。随着问题背景的复杂度增加，理论上也渐渐失去保证了，exploration的应用难度也渐渐加大。

14.2 Naive/Greedy Exploration

14.2.1 Greedy

一种最直接的探索方法就是贪心策略：每次选择当前“准确率”高的机器。我们可以去学习一个动作的好坏$\widehat{Q}_{t}(a)$，比如使用MC方法来计算平均reward（当然，也可以增量的进行更新）

\[\widehat{Q}_t(a)=\frac{1}{N_t(a)} \sum_{t=1}^T r_t \mathbf{1}(a_t=a)\]

然后，每次贪心的进行选择$a_{t}=\arg\max \widehat{Q}_{t}(a)$。咋一看，感觉还可以。但是如果一开始选到了一个次优的，就会一直贪心的选同一个，而不去尝试其他action。所以，greedy的regret是线性的，每次选择都会有错（因为太贪心了）。

14.2.2 $\epsilon-$greedy & Initialization

一个缓解贪心策略的方法就是$\epsilon-$greedy。这种方法会以一定的概率选择贪心action，以一定概率随机的选择其他action。也就是说，它也有一定概率陷入greedy策略的窘地，但是有小概率可以逃脱。在实际使用的时候，还有一个小的trick：在初始化模型的时候，将$\widehat{Q}(a)$设置成一个很大的值，$N(a)$也设置成很大的值。这么做的想法是：一个action是坏的，只有当证明他真的是坏的，并且，他会鼓励在一开始的时候，尽可能的多做探索。因为当初始值很大的时候，如果一个action a带来的reward很小，那么$\widehat{Q}(a)$就会降低。一旦它降低，那么下一次我们就会去尝试其他action，因为他们的$\widehat{Q}(a’)$可能更大。最后，虽然这种方法的效果会比纯贪心的方法好，但是他的regret也是线性的。

那么，基于贪心的方法能达到sublinear么？如果已知每一次的最优动作，那么基于贪心的方法是可以达到sub-linear的效果。这时候会要求$\epsilon$的值是动态改变的。（如果不知道最优动作，$\triangle_{a}$是计算不出来的）

\[\epsilon_t=\min(1, \frac{c\mid A \mid }{d^2t})\\ d=\min_{a \mid \triangle_a > 0} \triangle_i\\ c>0\]

这时候，算法的regret bound是sublinear的。但是，以上所有的方法，要让他们收敛到bound上，都需要很多次的实验，所以，在有限制次数的情况下，这些都是没啥理论保证的。

14.3 Upper Confidence Bound

Upper Confidence Bound，简称UCB。这个方法在介绍MCTS的时候用提到了，他在选择action的时候，还可靠了action的不确定性（带来10分的action V.S. 可能带来5到20分的action）。如下图所示，通过很多次的实验，我们计算出三个机器给的reward分布。一号机$Q(a_{1})$的均值大概在$2.5$，并且方差很小，也就说，选择一号机很大可能他会给出2.5的reward。同理二号机是2，三号机1.5。这时候应该如何选择呢？如果选择1号，那么大概率是2.5分，但是从2号或者3号得到大于2.5分的reward的概率是不小的，尤其是3号，他的不确定性最大，得高分的可能性也最大。UCB提供了一个综合考虑的策略，他认为不确定性越大的action，越应该去探索，有可能那会是更好的action。

随着实验的增加，我们就会越来越置信：

所以，UCB假设每一个动作都有一个置信度$U_{t}(a)$上限，这个置信度和观察次数有关。对于一个动作的观察次数$N_{t}(a)$越大，置信度应该越小。我们当前的估计值$\widehat{Q_{t}}(a)$和置信度$U_{t}(a)$一起决定了真实值的上界。即，$Q_{t}(a)\leq \widehat{Q_{t}}(a)+U_{t}(a)$。因此，在选择action的时候，需要一起考虑。通过最大化上界，选择出最有可能的动作。

\[a_t=\arg\max_a \widehat{Q}_t(a) + U_t(a)\]

根据Hoeffding不等式，他给出了随机变量的和与其期望值偏差的概率上限

UCB可以套用这个不等式来计算$U_{t}(a)$。套用下来就是

\[P\left(Q_t(a)>\widehat{Q}_t(a)+U_t(a)\right) \leq e^{-2N_t(a)U_t(a)^2}\]

假如我们希望这个bound不超过p（比如p=5%），那么根据$p=e^{-2N_{t}(a)U_{t}(a)^2}$，可以得到

\[U_t(a)=\sqrt{\frac{-\log p}{2N_t(a)}}\]

回想，这里的置信度和观察次数是有关的。对于一个动作的观察次数$N_{t}(a)$越大，置信度应该越小。所以，我们希望概率p是t的函数，比如$p=t^{-4}$，这时候有：

\[U_t(a)=\sqrt{\frac{2\log t}{N_t(a)}}\\ a_t=\arg\max_a \widehat{Q}_t(a) + \sqrt{\frac{2\log t}{N_t(a)}}\]

这个式子就很友善了，是在MCTS中访问子节点时候用到的指标。不过，在MCTS中，$N_{t}(a)$表示该节点被访问的次数，t表示这个节点的父节点被访问的次数。实际上$U_{t}(a)$的形式并不是局限于上面的这种形式，其他论文里也有人采用别的形式，比如：

\[U_t(a)=\sqrt{\frac{1}{N_t(a)}} \mbox{ 或者 } U_t(a)=\frac{1}{N_t(a)}\]

另外，UCB也是一个sublinear的方法。但是UCB在MDPs上的应用是有一点点bug的。UCB本身是用于bandits问题，而bandits的episode长度为1，所以，UCB没有考虑在MDPs中一条episode的数据之间的相互依赖。并且，处理一条episode的过程中，policy也可能是在更新的，但是UCB的$U_{t}(a)$在一条episode上是不变的。当然，这个问题很难处理，所以，UCB还是应用挺广的。

14.4 Posterior Sampling / Probability Matching

Posterior Sampling是一种以概率选择的方法，它在历史实验的情况下，根据action是最优action的概率来进行选择

\[\pi(a\mid h_t)=P(Q(a) > Q(a'), \forall a' \neq a \mid h_t)\]

这是一种Bayesian Bandits，在各个bandits的reward 分布是有先验的，所以，$\pi(a \mid h_{t})$是一个在历史实验数据$h_{t}$条件下的后验概率。举个栗子，假设bandits的reward的似然服从高斯分布$R_{a}(r)=N(r; \mu_{a}, \sigma_{a}^2)$，先验也是高斯，并且各个bandits之间是独立的（如下图）。那么，就可以求出均值和方差的后验分布，用后验值来选择action。比如可以用下式：

\[a_t= \arg\max \mu_a + \frac{c \sigma_a}{\sqrt{N_t(a)}}\]

上面的解法的后背是采用了Thompson Sampling的思想。Thompson Sampling是用来求解probability matching的方法：依概率随机选择动作，而这里的概率是指该动作是最优的动作的概率

\[\pi(a\mid h_t)=P(Q(a) > Q(a'), \forall a' \neq a \mid h_t)\\ =E_{R \mid h_t} \left[ \mathbf{1}(a=\arg\max_a Q(a)) \right]\]

详细的说，他的求解过程就是：

计算后验$P$（比如，上面的例子，我们算到了均值和方差的后验分布）
从后验 $P$中采样出reward分布（从每一个bandit的后验采样出一个均值和方差，这样每个bandits上的reward分布也就确定了）
选择动作 $a_{t}=\arg\max_{a} Q(a)$（比如采用UCB的方法来计算）
根据选择的结果，更新后验分布$P$

14.5 Information State Search

Information State Search是一个新的视角。他把bandits转变成了连续决策的过程。原始bandits是没有state的，这里给它加了一个Information state。所谓的information state $s$是指带一个历史信息的总和，即$s_{t}=f(h_{t})$。比如当$t=0$的时候，$s_{0}$表示一次都没有pull；如果$t=1$的时候，以一定的选择概率$P$，拉了一号，那么$s_{1}$就表示一号拉了一次，其他0次。所以这个又变成了一个MDP了：${S,A,P,R,\gamma}$

既然变成了传统的MDPs问题，我们就可以用model-free的方法（比如Q-learning）求出Q，或者用model-based RL的方法遍历出所有的情况，就像AlphaGo的MCTS一样。比如下图，一共有两个bandits，他们的reward有一定的先验分布，如果这时选择第一台机器（对应左分支），他可能给一个好的或者坏的reward，根据不同的reward，就可以更新第一台机器的reward分布，以此类推。这实际上就是一个Planning，当planning了很久之后（如果次数有限，那么就做有限次的Planning就好），就大概可以得到两台bandits的reward分布究竟长什么样子，那么也就可以做出好的选择。

如果上面的例子中的先验选择Beta分布 $Beta(\alpha_{a},\beta_{a}) $，其中$\alpha$表示坏reward，$\beta$表示好reward。那么他们的后验变化就可以表示成下图（暂时不动矩阵中的第二行有啥用。。）

这里具体的求解可以使用Gittins indices，也叫Bayes-Adaptive RL，他也是一种基于动态规划的算法。

14.6 Information Gain

基于信息增益的方法直接度量了一个action所带来的信息收益，以减小bandit的reward分布的不确定性。

\[IG(z,y\mid a) = E_y\left[ H(P(z))-H(P(z)\mid y) \mid a \right]\]

这里的y表示reward $r_{a}$，z表示bandits的reward分布的参数$\theta_{a}$。这个式子的含义是：根据做出action a，我们能收到一定的reward，那么，这个reward能降低当前a所作用的bandits上参数的多少不确定性，从而来衡量动作a的收益有多大。因此，我们可以这样选动作：希望找一个信息增益大的，并且与最优动作之间的差异小的动作。（这里假设了已知最优动作，所以才能计算$\triangle_{t}(a)$）

\[\arg\min_a \frac{\triangle_t(a)^2}{IG(\theta_a, r_a\mid a)}\]

14.7 RL in Action

Multi-armed bandits相比于RL来说，问题简单了不少。本部分主要就RL的exploration方法做一个简述。总的来说，上面提到的方法在RL中都可以应用。比如基于Naive method或者UCB的方法，但首先要解决的问题是怎么对某个状态的访问次数进行计数。这个问题在连续action space下，用常规的方法是“数”不过来的。

14.7.1 How to count $N_{t}(a)$ or $N_{t}(s)$

对于离散空间下的action/state还可以单纯的通过计数的方式统计，但是在连续空间下，同一个action/state重复出现的概率是等于0的，但是不同的action/state之间可能是很相似的。对于连续空间，我们可以使用deep network来学习出pseudo-count，记为$P_\theta(s)$或者$P_\theta(s,a)$。这样，相似的输入，我们可以保证有相似输出（count）。

一种方案是将连续转变成离散，在新的离散空间来count。这种手段比较多，比如聚类，Hash等等。我们首先得到state的feature，然后通过聚类或者Hash的方法把它映射到簇或者partition bin中。这种方法很粗糙，而且和离散空间的大小有关系。但是有用Hash来做的文献表明，效果是挺好的，如下图所示。（聚类的方法不知道有没有文献支持）

还有一种不同的思路：如果，在某个时刻，$P(s)$是等于下面第一个式子，在下时刻又观察到s的时候，我们用第二个式子表示count的ratio。其中n是总的实验次数，$N(s)$表示n中观察到状态s的次数

\[P_{\theta}(s)=\frac{N(s)}{n}\\ P_{\theta'}(s)=\frac{N(s)+1}{n+1}\]

有了这两个式子，我们就可以反推出$N(s)$：

\[N(s)=nP_\theta(s) = \frac{1-P_{\theta'}(s)}{P_{\theta'}(s)-P_\theta(s)}P_\theta(s)^2\]

所以，我们可以得到计数的一个伪代码：

简单的说，就是找到$P_\theta(s)$，计算出$N(s)$就ok了。问题是怎么计算$P_\theta(s)$？其中一个方法是通过构建一个分类器来实现density value的输出。

EX2: Exploration with Exemplar Models for Deep Reinforcement Learning

他的基本假设是：如果一个状态是比较陌生的，那么他会很容易被分类器与之前的状态分开。所以，首先以之前所有的state作为负类，以当前state作为一个正类，训练一个分类器。那么以下面这个分类的难易程度来近似$P_\theta(s)$。其中$D_{s}(s)$表示关于状态s的分类器，把状态s分成状态s的概率。（是的，我没有打错字）

\[P_\theta(s) = \frac{1-D_s(s)}{D_s(s)}\]

论文说，当状态s已经在以前的某个时刻经历过，那么，最优分类器$D_{s}(s)$其实不等于1，而是等于$D_{s}(s)=\frac{1}{1+P(s)}$，所以才会以上面的式子来近似计算$P_\theta(s)$

14.7.2 UCB in RL

UCB的方法基本和所有的RL算法都很兼容，这时候只需要将reward设置为$r(s,a)+ e \sqrt{\frac{2\log t}{N(a)} }$。这里$e$是两个部分的融合权重，怎么设置就需要调参咯

14.7.3 Posterior sampling in RL

posterior sample与RL的结合方式是通过Off-policy。比如在Q-learning，我们其实并不关心要基于那个Q函数来求max，选action。所以可以吧这个Q当做是一个从posterior 中采样出来的样本。这么做

14.7.4 Naive Method in RL

使用$\epsilon-$greedy的方法，同时结合那个特殊的初始化方法，然后就可以正常的跑Q-learning, sarsa, MC等等model-free RL方法。
或者采用model-based方法，在学习reward和transition的时候，初始化每个状态的reward都最大。然后随着学习的进行，用table lookup的方法统计和学习真正的reward。这个方法和有特殊初始化的$\epsilon-$greedy方法如出一辙，该算法叫RMax